题目内容
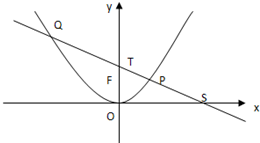 如图,P是抛物线C:x2=2y上一点,F为抛物线的焦点,直线l过点P且与抛物线交于另一点Q,已知P(x1,y1),Q(x2,y2).
如图,P是抛物线C:x2=2y上一点,F为抛物线的焦点,直线l过点P且与抛物线交于另一点Q,已知P(x1,y1),Q(x2,y2).(1)若l经过点F,求弦长|PQ|的最小值;
(2)设直线l:y=kx+b(k≠0,b≠0)与x轴交于点S,与y轴交于点T
①求证:
| |ST| |
| |SP| |
| |ST| |
| |SQ| |
| 1 |
| y1 |
| 1 |
| y2 |
②求
| |ST| |
| |SP| |
| |ST| |
| |SQ| |
分析:(1)由抛物线的方程求出抛物线的焦点,写出过焦点的直线l的方程,和抛物线方程联立后化为关于x的一元二次方程,利用根与系数关系求出P,Q的横坐标的和,借助于抛物线的定义把弦长|PQ|转化为两点横坐标的代数式,利用不等式求弦长|PQ|的最小值;
(2)①分别过P,Q作PP′⊥x轴,QQ′⊥x轴,利用平行线截线段成比例定理把要证的等式的左边转化为直线在y轴上的截距与点的纵坐标的比,从而得到要证得结论;
②联立
,消去x,得y2-2(k2+b)y+b2=0,利用根与系数关系得到P,Q两点的纵坐标的和与积,结合基本不等式代入①后得到结论,或利用分类讨论的方法求解
+
的取值范围.
(2)①分别过P,Q作PP′⊥x轴,QQ′⊥x轴,利用平行线截线段成比例定理把要证的等式的左边转化为直线在y轴上的截距与点的纵坐标的比,从而得到要证得结论;
②联立
|
| |ST| |
| |SP| |
| |ST| |
| |SQ| |
解答:(1)解:∵F为抛物线的焦点,∴F(0,
)
设直线l:y=kx+
,
联立
,得x2-2kx-1=0(﹡)
则|PQ|=|PF|+|QF|=(y1+
)+(y2+
)=y1+y2+1=k(x1+x2)+2.
由(﹡)得x1+x2=2k,带入上式得|PQ|=2k2+2≥2,当仅当k=0时|PQ|的最小值为2;
(2)证明:如图,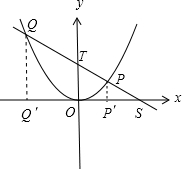
①分别过P,Q作PP′⊥x轴,QQ′⊥x轴,垂足分别为P′,Q′,
则
+
=
+
=
+
=|b|(
+
)
②联立
,消去x,得y2-2(k2+b)y+b2=0(﹟)
则y1+y2=2(k2+b),y1y2=b2.
(方法1)
而
+
=|b|(
+
)≥2|b|
=2|b|
=2
而y1,y2可取一切不相等的正数∴
+
的取值范围为(2,+∞).
(方法2)
+
=|b|(
+
)=|b|
=|b|
当b>0时,上式=
+2>2;
当b<0时,上式=
.
由(﹟)式△>0得k2+2b>0即k2>-2b
于是
+
>
=2
综上,
+
的取值范围为(2,+∞).
| 1 |
| 2 |
设直线l:y=kx+
| 1 |
| 2 |
联立
|
则|PQ|=|PF|+|QF|=(y1+
| 1 |
| 2 |
| 1 |
| 2 |
由(﹡)得x1+x2=2k,带入上式得|PQ|=2k2+2≥2,当仅当k=0时|PQ|的最小值为2;
(2)证明:如图,

①分别过P,Q作PP′⊥x轴,QQ′⊥x轴,垂足分别为P′,Q′,
则
| |ST| |
| |SP| |
| |ST| |
| |SQ| |
| |OT| |
| |P/P| |
| |OT| |
| |Q/Q| |
| |b| |
| |y1| |
| |b| | ||
|y
|
| 1 |
| y1 |
| 1 |
| y2 |
②联立
|
则y1+y2=2(k2+b),y1y2=b2.
(方法1)
而
| |ST| |
| |SP| |
| |ST| |
| |SQ| |
| 1 |
| y1 |
| 1 |
| y2 |
|
|
而y1,y2可取一切不相等的正数∴
| |ST| |
| |SP| |
| |ST| |
| |SQ| |
(方法2)
| |ST| |
| |SP| |
| |ST| |
| |SQ| |
| 1 |
| y1 |
| 1 |
| y2 |
| y1+y2 |
| y1y2 |
| 2(k2+b) |
| b2 |
当b>0时,上式=
| 2k2 |
| b |
当b<0时,上式=
| 2(k2+b) |
| -b |
由(﹟)式△>0得k2+2b>0即k2>-2b
于是
| |ST| |
| |SP| |
| |ST| |
| |SQ| |
| 2(-2b+b) |
| -b |
综上,
| |ST| |
| |SP| |
| |ST| |
| |SQ| |
点评:本题考查了直线与圆锥曲线的综合题,考查了数学转化思想方法和分类讨论的数学思想方法,直线与圆锥曲线关系问题,常采用直线与曲线联立,根据方程的根与系数的关系求解,这是处理这类问题的最为常用的方法,但圆锥曲线的特点是计算量比较大,要求考生具备较强的运算推理的能力,是难题.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
 如图,P是抛物线C:y=
如图,P是抛物线C:y= 如图,P是抛物线C:y=
如图,P是抛物线C:y=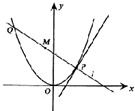 如图,P是抛物线C:y=
如图,P是抛物线C:y=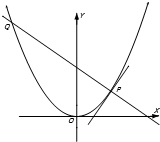 如图,P是抛物线C:y=
如图,P是抛物线C:y=