题目内容
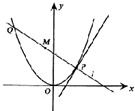 如图,P是抛物线C:y=
如图,P是抛物线C:y=| 1 | 2 |
(Ⅰ)当点P的横坐标为2时,求直线l的方程;
(Ⅱ)当点P在抛物线C上移动时,求线段PQ中点M的轨迹方程,并求点M到x轴的最短距离.
分析:(1)由于直线l过点P并与抛物线C在点P的切线垂直,要求求直线l的方程,我们可以根据点P的横坐标为2,求出点P的坐标,并求出P点处函数的导数值,即过P点切线的斜率,进而得到直线l的斜率,代入点斜式方程进行求解.
(2)方法一,求线段PQ中点M的轨迹方程,我们可以分别求出直线与抛物线两交点的坐标,代入中点公式进行化简,得到变量x,y之间的关系,即轨迹方程;
方法二:将直线方程代入抛物线的方程,再结合韦达定理(根与系数关系)对式子进行化简,探究变量x,y之间的关系,即轨迹方程.
(2)方法一,求线段PQ中点M的轨迹方程,我们可以分别求出直线与抛物线两交点的坐标,代入中点公式进行化简,得到变量x,y之间的关系,即轨迹方程;
方法二:将直线方程代入抛物线的方程,再结合韦达定理(根与系数关系)对式子进行化简,探究变量x,y之间的关系,即轨迹方程.
解答:解:(Ⅰ)把x=2代入y=
x2,得y=2,
∴点P坐标为(2,2).
由y=
x2,①
得y'=x,
∴过点P的切线的斜率k切=2,
直线l的斜率kl=-
=-
,
∴直线l的方程为y-2=-
(x-2),
即x+2y-6=0.
(Ⅱ)设P(x0,y0),则y0=
.
∵过点P的切线斜率k切=x0,
当x0=0时不合题意,x0≠0.
∴直线l的斜率kl=-
=-
,
直线l的方程为y-
=-
(x-x0).②
方法一:联立①②消去y,得x2+
x-x02-2=0.设Q(x1,y1),M(x,y).
∵M是PQ的中点,
∴
消去x0,得y=x2+
+1(x≠0)就是所求的轨迹方程.
由x≠0知x2>0,∴y=x2+
+1≥2
+1=
+1.
上式等号仅当x2=
,即x=±4
时成立,所以点M到x轴的最短距离是
+1.
方法二:
设Q(x1,y1),M(x,y).则
由y0=
x02,y1=
x12,x=
,
∴y0-y1=
x02-
x12=
(x0+x1)(x0-x1)=x(x0-x1),
∴x=
=kl=-
,∴x0=-
,
将上式代入②并整理,得y=x2+
+1(x≠0)就是所求的轨迹方程.
由x≠0知x2>0,∴y=x2+
+1≥2
+1=
+1.
上式等号仅当x2=
,即x=±4
时成立,所以点M到x轴的最短距离是
+1.
| 1 |
| 2 |
∴点P坐标为(2,2).
由y=
| 1 |
| 2 |
得y'=x,
∴过点P的切线的斜率k切=2,
直线l的斜率kl=-
| 1 |
| k切 |
| 1 |
| 2 |
∴直线l的方程为y-2=-
| 1 |
| 2 |
即x+2y-6=0.
(Ⅱ)设P(x0,y0),则y0=
| 1 |
| 2 |
| x | 2 0 |
∵过点P的切线斜率k切=x0,
当x0=0时不合题意,x0≠0.
∴直线l的斜率kl=-
| 1 |
| k切 |
| 1 |
| x0 |
直线l的方程为y-
| 1 |
| 2 |
| x | 2 0 |
| 1 |
| x0 |
方法一:联立①②消去y,得x2+
| 2 |
| x0 |
∵M是PQ的中点,
∴
|
消去x0,得y=x2+
| 1 |
| 2x2 |
由x≠0知x2>0,∴y=x2+
| 1 |
| 2x2 |
x2•
|
| 2 |
上式等号仅当x2=
| 1 |
| 2x2 |
|
| 2 |
方法二:
设Q(x1,y1),M(x,y).则
由y0=
| 1 |
| 2 |
| 1 |
| 2 |
| x0+x1 |
| 2 |
∴y0-y1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴x=
| y0-y1 |
| x0-x1 |
| 1 |
| x0 |
| 1 |
| x |
将上式代入②并整理,得y=x2+
| 1 |
| 2x2 |
由x≠0知x2>0,∴y=x2+
| 1 |
| 2x2 |
x2•
|
| 2 |
上式等号仅当x2=
| 1 |
| 2x2 |
|
| 2 |
点评:本题主要考查直线、抛物线、不等式等基础知识,求轨迹方程的方法,解析几何的基本思想和综合解题能力.在使用点斜式表示过定点的直线方程时,一定要注意它不能表示斜率不存在的直线,此时与它垂直的直线斜率为0,故在使用前要对这种情况进行讨论.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 如图,P是抛物线C:y=
如图,P是抛物线C:y=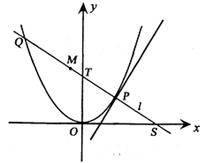 如图,P是抛物线C:y=
如图,P是抛物线C:y=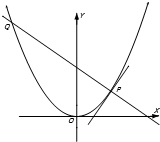 如图,P是抛物线C:y=
如图,P是抛物线C:y=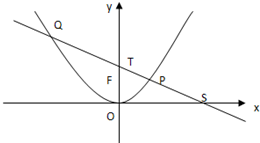 如图,P是抛物线C:x2=2y上一点,F为抛物线的焦点,直线l过点P且与抛物线交于另一点Q,已知P(x1,y1),Q(x2,y2).
如图,P是抛物线C:x2=2y上一点,F为抛物线的焦点,直线l过点P且与抛物线交于另一点Q,已知P(x1,y1),Q(x2,y2).