题目内容
【题目】已知函数 ![]()
(1)求函数f(x)在 ![]() 上的最大值与最小值;
上的最大值与最小值;
(2)已知 ![]() ,x0∈(
,x0∈( ![]() ,
, ![]() ),求cos4x0的值.
),求cos4x0的值.
【答案】
(1)解:函数 ![]()
化简可得:3 ![]() +
+ ![]() sin2x﹣
sin2x﹣ ![]()
= ![]() ﹣
﹣ ![]() cos2x×
cos2x× ![]() +
+ ![]() ×
× ![]() sin2x+
sin2x+ ![]() sin2x﹣
sin2x﹣ ![]() ﹣
﹣ ![]() cos2x
cos2x
= ![]() sin2x﹣cos2x+
sin2x﹣cos2x+ ![]()
=2sin(2x﹣ ![]() )+
)+ ![]() .
.
∵x∈ ![]() 上,
上,
∴2x﹣ ![]() ∈[-
∈[- ![]() ,
, ![]() ].
].
∴sin(2x﹣ ![]() )∈[
)∈[ ![]() ,1].
,1].
函数f(x)在 ![]() 上的最大值为
上的最大值为 ![]() ,最小值为
,最小值为 ![]()
(2)解:∵ ![]() ,即2sin(4x0﹣
,即2sin(4x0﹣ ![]() )+
)+ ![]() =
= ![]()
sin(4x0﹣ ![]() )=
)= ![]()
∵x0∈( ![]() ,
, ![]() ),
),
4x0﹣ ![]() ∈[
∈[ ![]() ,π],
,π],
∴cos(4x0﹣ ![]() )=
)= ![]() .
.
cos4x0=cos[4x0﹣ ![]() )+
)+ ![]() ]=cos(4x0﹣
]=cos(4x0﹣ ![]() )cos
)cos ![]() ﹣sin(4x0﹣
﹣sin(4x0﹣ ![]() )sin
)sin ![]() =
= ![]() ×
× ![]() ﹣
﹣ ![]() =
= ![]()
【解析】(1)利用二倍角和辅助角公式基本公式将函数化为y=Asin(ωx+φ)的形式,求出内层函数的取值范围,结合三角函数的图象和性质,求出f(x)的取值最大和最小值;(2)利用 ![]() ,x0∈(
,x0∈( ![]() ,
, ![]() ),代入化简,找出与cos4x0的值关系,可求解.
),代入化简,找出与cos4x0的值关系,可求解.

【题目】随着资本市场的强势进入,互联网共享单车“忽如一夜春风来”,遍布了一二线城市的大街小巷.为了解共享单车在![]() 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中抽取了200人进行抽样分析,得到表格:(单位:人)
市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中抽取了200人进行抽样分析,得到表格:(单位:人)
经常使用 | 偶尔或不用 | 合计 | |
30岁及以下 | 70 | 30 | 100 |
30岁以上 | 60 | 40 | 100 |
合计 | 130 | 70 | 200 |
(1)根据以上数据,能否在犯错误的概率不超过0.15的前提下认为![]() 市使用共享单车情况与年龄有关?
市使用共享单车情况与年龄有关?
(2)现从所抽取的30岁以上的网友中利用分层抽样的方法再抽取5人.
(i)分别求这5人中经常使用、偶尔或不用共享单车的人数;
(ii)从这5人中,再随机选出2人赠送一件礼品,求选出的2人中至少有1人经常使用共享单车的概率.
参考公式: 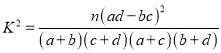 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 3.841 | 5.024 | 6.635 |
