题目内容
若R上的奇函数 的图象关于直线
的图象关于直线 对称,且当
对称,且当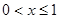 时,
时, ,则方程
,则方程 在区间
在区间 内的所有实数根之和为( )
内的所有实数根之和为( )
| A.4020 | B.4022 | C.4024 | D.4026 |
B
解析试题分析:∵函数y=f(x)的图象关于直线x=1对称,∴f(2-x)=f(x),又y=f(x)为奇函数,∴f(x+2)=f(-x)=-f(x),∴f(x+4)=-f(x+2)=f(x),即f(x)的周期为4,,又定义在R上的奇函数,故f(0)=0,,∵f(x)=f(0)+ ,∴f(x)=
,∴f(x)= ,∵0<x≤1时,f(x)=log2x≤0,∴f(x)=
,∵0<x≤1时,f(x)=log2x≤0,∴f(x)= 在(0,1)内没有一实根,在(-1,0)内有一实数根x1,又函数f(x)的图象关于直线x=1对称,∴f(x)=
在(0,1)内没有一实根,在(-1,0)内有一实数根x1,又函数f(x)的图象关于直线x=1对称,∴f(x)= 在(2,3)有一个实根x2,且x1+x2=2;
在(2,3)有一个实根x2,且x1+x2=2;
∵f(x)的周期为4,当2010<x<2012时,函数的图象与2<x<4的图象一样,∴原方程在区间(2010,2012)内的实根有2个,设为a,b,则 =2011∴a+b=4022,故选B
=2011∴a+b=4022,故选B
考点:本题主要考查根的存在性及根的个数判断及奇偶函数图象的对称性,关键在于判断f(x)的周期为4,再结合0<x≤1时,f(x)=log2x与奇函数f(x)的图象关于直线x=1对称,数形结合予以解决,属于中档题.
点评:解决该试题的关键是由奇函数f(x)的图象关于直线x=1对称可得f(x+4)=f(x),再利用f(0)=0,及0<x≤1时,f(x)=log2x,数形结合,可求得方程f(x)= +f(0)=
+f(0)= 在区间(2010,20121)内的所有实根之和.
在区间(2010,20121)内的所有实根之和.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案函数 是偶函数,它在
是偶函数,它在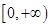 上是减函数.若
上是减函数.若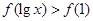 ,则
,则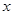 的取值范围是
的取值范围是
A.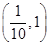 | B.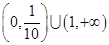 |
C.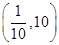 | D.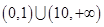 |
已知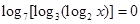 ,那么
,那么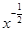 等于( )
等于( )
A.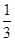 | B.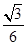 | C.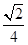 | D.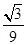 |
函数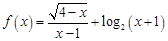 的定义域为( )
的定义域为( )
A.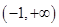 | B.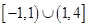 | C.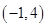 | D.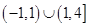 |
若函数 唯一的零点在区间(1,3)、(1,4)、(1,5)内,那么下列命题中错误的是( )
唯一的零点在区间(1,3)、(1,4)、(1,5)内,那么下列命题中错误的是( )
A.函数 在(1,2)或 在(1,2)或 内有零点 内有零点 | B.函数 在(3,5)内无零点 在(3,5)内无零点 |
C.函数 在(2,5)内有零点 在(2,5)内有零点 | D.函数 在(2,4)内不一定有零点. 在(2,4)内不一定有零点. |
若函数
A. | B. |
C. | D. |
设函数
 的图象关于直线
的图象关于直线 及直线
及直线 对称,且
对称,且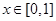 时,
时, ,则
,则 ( )
( )
A. | B. | C. | D. |
设偶函数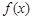 满足
满足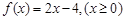 ,则不等式
,则不等式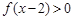 的解集是( )
的解集是( )
A.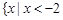 或 或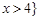 | B.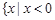 或 或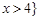 |
C.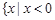 或 或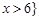 | D.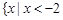 或 或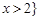 |
 ;②
;② ;③
;③ ;④
;④ .则下列函数图象(在第一象限部分)从左到右依次与函数序号的正确对应顺序是
.则下列函数图象(在第一象限部分)从左到右依次与函数序号的正确对应顺序是 