题目内容
(本题满分12分)如图所示,在棱长为4的正方体ABCD—A1B1C1D1中,点E是棱CC1的中点。

(I)求三棱锥D1—ACE的体积;
(II)求异面直线D1E与AC所成角的余弦值;
(III)求二面角A—D1E—C的正弦值。

(I)求三棱锥D1—ACE的体积;
(II)求异面直线D1E与AC所成角的余弦值;
(III)求二面角A—D1E—C的正弦值。
(I)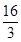 ;(II)
;(II)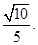 (III)
(III)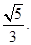
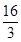 ;(II)
;(II)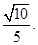 (III)
(III)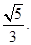
试题分析:(I)
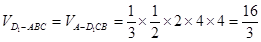 …………3分
…………3分(II)取DD1的中点F,连结FC,则D1E//FC,
∴∠FCA即为异面直线D1E与AC
所成角或其补角。 …………5分
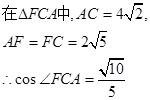
∴异面直线D1E与AC所成角的余弦值为
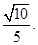 …………7分
…………7分(III)过点D作DG⊥D1E于点G,连接AG,由AD⊥面D1DCC1,
∴AD⊥D1E
又∵DG⊥D1E,∴D1E⊥面ADG
∴D1E⊥AG,则∠AGD为二面角A—D1E—C的平面角 ……9分
∵D1E·DG=DD1·CD,
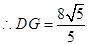
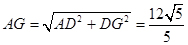
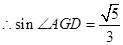 ,
,二面角A—D1E—C的正弦值为
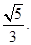 …………12分
…………12分法二:(I)同法一 ………………3分
(II)以D为原点,分别以DA,DC,DD1为ox,oy,oz轴建立空间直角坐标系。
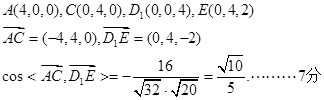
(III)显然
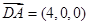 是平面D1DCE的法向量,
是平面D1DCE的法向量,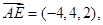 设平面D1AE的一个法向量为
设平面D1AE的一个法向量为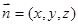
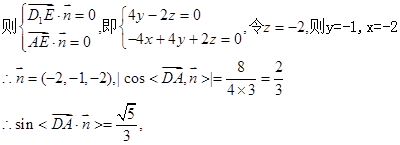
二面角A—D1E—C的正弦值为
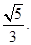 …………12分
…………12分点评:求异面直线所成的角,解题的关键是:首先正确的建立空间直角坐标系,然后可将异面直线所成的角转化为所对应的向量的夹角或其补角;而对于利用向量法求线面角关键是正确求解平面的一个法向量。注意计算要仔细、认真。

练习册系列答案
相关题目
 中,
中,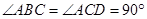 ,
,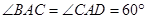 ,
,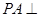 平面
平面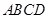 ,
,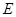 为
为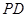 的中点,
的中点,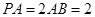 .
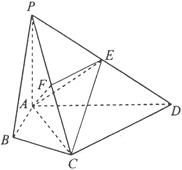
.
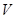 ;
;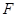 为
为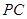 的中点,求证:平面
的中点,求证:平面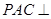 平面
平面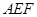 ;
;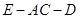 的大小。.
的大小。.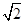 倍,P为侧棱SD上的点.
倍,P为侧棱SD上的点.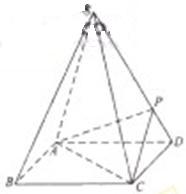
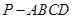 中,底面
中,底面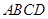 是矩形,
是矩形,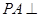 平面
平面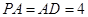 ,
,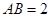 .以
.以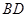 的中点
的中点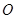 为球心、
为球心、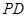 于点
于点 .
.
 ;
; 与平面
与平面 的正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC=
的正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC=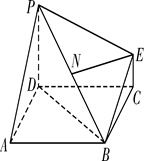
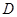 到平面
到平面 的距离.
的距离.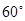 的二面角内的一个球与二面角的两个面的切点到棱的距离都是6,则这个球的半径为_______.
的二面角内的一个球与二面角的两个面的切点到棱的距离都是6,则这个球的半径为_______.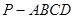 中,底面
中,底面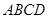 是正方形,侧棱
是正方形,侧棱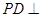 底面
底面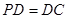 ,
, 是
是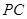 的中点,作
的中点,作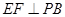 交
交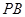 于点
于点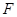
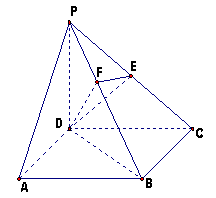
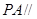 平面
平面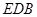 .
. 平面
平面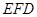 .
.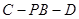 的大小.
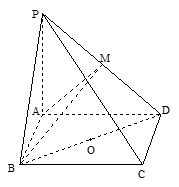
的大小.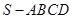 的侧棱长与底面边长都相等,
的侧棱长与底面边长都相等,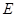 是
是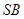 的中点,则
的中点,则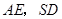 所成的角的余弦值为( )
所成的角的余弦值为( )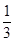
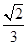
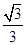
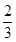
 ,β,γ,给出下列命题:
,β,γ,给出下列命题: ,则
,则