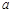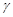题目内容
(本小题满分16分)
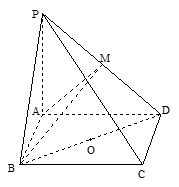
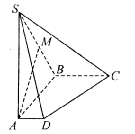
如图,在四棱锥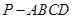 中,底面
中,底面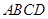 是矩形,
是矩形,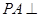 平面
平面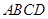 ,
,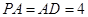 ,
,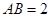 .以
.以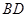 的中点
的中点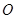 为球心、
为球心、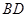 为直径的球面切
为直径的球面切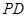 于点
于点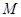 .
.
(1)求证:PD⊥平面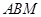 ;
;
(2)求直线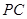 与平面
与平面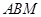 所成的角的正弦值;
所成的角的正弦值;
(3)求点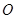 到平面
到平面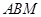 的距离.
的距离.
如图,在四棱锥
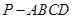 中,底面
中,底面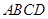 是矩形,
是矩形,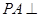 平面
平面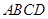 ,
,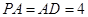 ,
,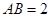 .以
.以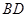 的中点
的中点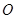 为球心、
为球心、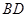 为直径的球面切
为直径的球面切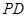 于点
于点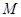 .
.
(1)求证:PD⊥平面
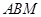 ;
;(2)求直线
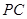 与平面
与平面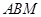 所成的角的正弦值;
所成的角的正弦值;(3)求点
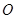 到平面
到平面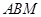 的距离.
的距离.(1)先证 ,推出
,推出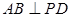 ,证明
,证明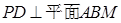 ;
;
(2)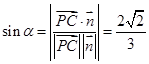 ;(3)
;(3)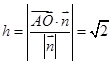
 ,推出
,推出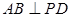 ,证明
,证明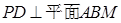 ;
;(2)
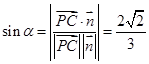 ;(3)
;(3)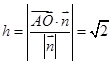
试题分析:(1)证:依题设,
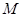 在以
在以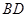 为直径的球面上,则
为直径的球面上,则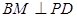 ,……2分
,……2分因为
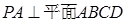 ,则
,则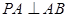 ,又
,又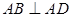 ,
,所以
 ,则
,则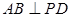 , ……4分
, ……4分因此有
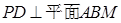 , ……5分
, ……5分(2)如图所示,建立空间直角坐标系,则
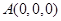 ,
,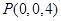 ,
,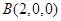 ,
,  ,
,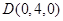 ,
,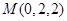 , ……8分
, ……8分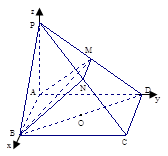
设平面
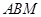 的一个法向量
的一个法向量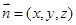 ,由
,由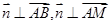 可得:
可得: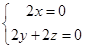 ,
,令
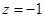 ,则
,则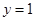 ,即
,即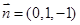 . ……10分
. ……10分设所求角为
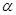 ,则
,则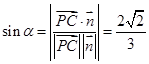 , ……12分
, ……12分(3)设所求距离为
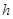 ,由
,由 ,得:
,得: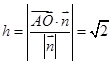 ……16分
……16分点评:典型题,立体几何中平行、垂直关系的证明及角的计算问题是高考中的必考题,通过建立适当的坐标系,应用空间向量,可使问题简化。

练习册系列答案
相关题目
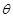 ,求sin
,求sin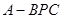 中,
中, ,
, ,
,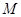 为
为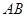 中点,
中点,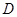 为
为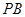 中点,且
中点,且 为正三角形.
为正三角形.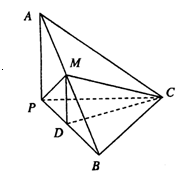
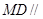 平面
平面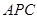 .
.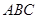 ⊥平面
⊥平面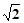 ,D是A1B1中点.
,D是A1B1中点.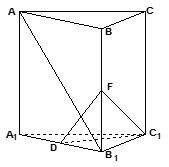
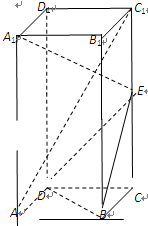
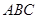 为底面的直棱柱被平面
为底面的直棱柱被平面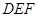 所截而得.
所截而得. 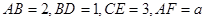 ,
,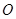 为
为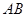 的中点.
的中点.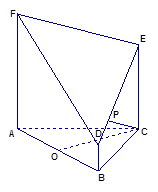
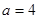 时,求平面
时,求平面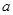 为何值时,在棱
为何值时,在棱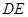 上存在点
上存在点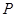 ,使
,使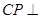 平面
平面
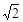 ,∠BAC=30°,若它们的斜边AB重合,让三角板ABD以AB为轴转动,则下列说法正确的是 .
,∠BAC=30°,若它们的斜边AB重合,让三角板ABD以AB为轴转动,则下列说法正确的是 .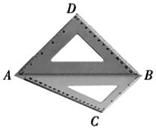
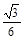 .
.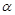 、
、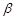 ,能判定
,能判定