题目内容
【题目】一缉私艇巡航至距领海边界线l(一条南北方向的直线)3.8海里的A处,发现在其北偏东30°方向相距4海里的B处有一走私船正欲逃跑,缉私艇立即追击.已知缉私艇的最大航速是走私船最大航速的3倍.假设缉私艇和走私船均按直线方向以最大航速航行.(参考数据: ![]() °
° ![]() ,
, ![]() )
)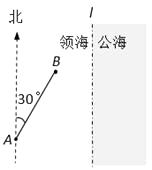
(1)若走私船沿正东方向逃离,试确定缉私艇的追击方向,使得用最短时间在领海内拦截成功;
(2)问:无论走私船沿何方向逃跑,缉私艇是否总能在领海内成功拦截?并说明理由.
【答案】
(1)
解:(1)设缉私艇在 ![]() 处与走私船相遇(如图甲),
处与走私船相遇(如图甲),

依题意, ![]() .
.
在△ ![]() 中,由正弦定理得,
中,由正弦定理得,
![]()
![]()
![]() .
.
因为 ![]() °
° ![]() ,所以
,所以 ![]() °.
°.
从而缉私艇应向北偏东 ![]() 方向追击.
方向追击.
在△ ![]() 中,由余弦定理得,
中,由余弦定理得,
![]() ,
,
解得 ![]()
![]() .
.
又B到边界线l的距离为 ![]() .
.
因为 ![]() ,所以能在领海上成功拦截走私船.
,所以能在领海上成功拦截走私船.
答:缉私艇应向北偏东 ![]() 方向追击;
方向追击;
(2)
解:如图乙,以 ![]() 为原点,正北方向所在的直线为
为原点,正北方向所在的直线为 ![]() 轴建立平面直角坐标系
轴建立平面直角坐标系 ![]() .
.
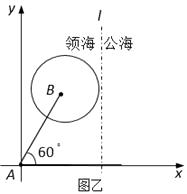
则 ![]() ,设缉私艇在
,设缉私艇在 ![]() 处(缉私艇恰好截住走私船的位置)与走私船相遇,则
处(缉私艇恰好截住走私船的位置)与走私船相遇,则 ![]() ,即
,即 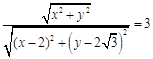 .
.
整理得, ![]() ,
,
所以点 ![]() 的轨迹是以点
的轨迹是以点 ![]() 为圆心,
为圆心, ![]() 为半径的圆.
为半径的圆.
因为圆心 ![]() 到领海边界线
到领海边界线 ![]() :
: ![]() 的距离为1.55,大于圆半径
的距离为1.55,大于圆半径 ![]() ,
,
所以缉私艇能在领海内截住走私船.
答:缉私艇总能在领海内成功拦截走私船.
【解析】(1) 假设在C点能拦截,由BC、AC关系算出∠BAC,再由余弦定理算出BC判断BC与B到边界的距离。(2)设出拦截点的坐标,根据 ![]() ,用两点间距离公式分别表示PA、PB可得一个圆,然后比较点B到边界的距离与半径的大小。
,用两点间距离公式分别表示PA、PB可得一个圆,然后比较点B到边界的距离与半径的大小。

练习册系列答案
相关题目


