题目内容
【题目】[选修4－4：坐标系与参数方程]
在直角坐标系
中，曲线
的参数方程为
（
为参数）；以原点
极点，以
轴正半轴为极轴，建立极坐标系，曲线
的极坐标方程为
.
⑴ 求曲线的普通方程与曲线的直角坐标方程；
⑵ 试判断曲线与是否存在两个交点，若存在求出两交点间的距离；若不存在，说明理由.
【答案】(1)曲线
：
，曲线
：
；(2)
.
【解析】
试题(1) 根据参数方程与普通方程的关系，对于曲线消去参数可得：，再根据极坐标方程与直角坐标方程的关系，对于曲线可转化为：；(2) 根据题意显然曲线：为直线，则其参数方程可写为
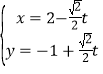（为参数）与曲线：联立，可知
，所以与存在两个交点，由
，
，得
.
试题解析：(1) 对于曲线有，对于曲线有.(5分)
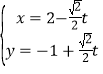(2) 显然曲线：为直线，则其参数方程可写为（为参数）与曲线：联立，可知，所以与存在两个交点，
由，，得. (10分)
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
【题目】为普及学生安全逃生知识与安全防护能力，某学校高一年级举办了安全知识与安全逃生能力竞赛，该竞赛分为预赛和决赛两个阶段，预赛为笔试，决赛为技能比赛，现将所有参赛选手参加笔试的成绩（得分均为整数，满分为
分）进行统计，制成如下频率分布表.
分数（分数段） | 频数（人数） | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
（1）求表中
，
，
，
，
的值；
（2）按规定，预赛成绩不低于
分的选手参加决赛.已知高一（2）班有甲、乙两名同学取得决赛资格，记高一（2）班在决赛中进入前三名的人数为
，求的分布列和数学期望.
