题目内容
9．求（1+3x+3x2+x3）10展开式中含x3的项．分析 根据（1+3x+3x2+x3）10=（1+x）30 的通项公式为Tr+1=${C}_{30}^{r}$•xr，可得展开式中含x3的项．
解答 解：（1+3x+3x2+x3）10=（1+x）30 的通项公式为Tr+1=${C}_{30}^{r}$•xr，
故令r=3可得展开式中含x3的项为 T4=${C}_{30}^{3}$•x3．
点评 本题主要考查二项式定理的应用，二项式系数的性质，二项式展开式的通项公式，属于基础题．
练习册系列答案
相关题目
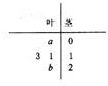如图所示是某组数据的茎叶图，已知该组数据的平均数为$\frac{23}{2}$，ab=1（a，b∈R），则$\frac{a}{2}sin2x+bco{s}^{2}x-\frac{b}{2}$的最大值为$\frac{\sqrt{2}}{2}$．