题目内容
17.已知a∈R,解关于x的不等式2x2-(2+a)x+a≤0.分析 求出不等式对应的方程的实数解,由此讨论a的取值,写出所对应的原不等式的解集即可.
解答 解:不等式2x2-(2+a)x+a≤0可化为(x-1)(2x-a)≤0,
即(x-1)(x-$\frac{a}{2}$)≤0,
它所对应的方程(x-1)(x-$\frac{a}{2}$)=0的解为1和$\frac{a}{2}$;
当a>2,即$\frac{a}{2}$>1时,原不等式的解集为{x|1≤x≤$\frac{a}{2}$};
当a=2,即$\frac{a}{2}$=1时,原不等式的解集为{x|x=1};
当a<2,即$\frac{a}{2}$<1时,原不等式的解集为{x|$\frac{a}{2}$≤x≤1}.
点评 本题考查了含有字母系数的一元二次不等式的解法与应用问题,解题时需要对字母系数进行讨论,
是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.设全集I=R,集合A={y|y=x2-2},B={x|x<3},则(∁1A)∩B=( )
| A. | {x|x<-2} | B. | {x|x≤-2} | C. | {x|x<3} | D. | {x|-2≤x<3} |
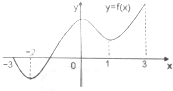 如图是定义在区间[-3,3]上的函数y=f(x)的图象,研究下列问题:
如图是定义在区间[-3,3]上的函数y=f(x)的图象,研究下列问题: