题目内容
已知函数f(x)=4sin2(x+)+4sin2x-(1+2),x∈R.
(1)求函数f(x)的最小正周期和图象的对称中心;
(2)求函数f(x)在区间上的值域.
(1)求函数f(x)的最小正周期和图象的对称中心;
(2)求函数f(x)在区间上的值域.
依题意得f(x)
=4sin2(x+)+4sin2x-(1+2)
=2[1-cos(2x+)]-2cos2x-1=4sin(2x-)+1.
(1)函数f(x)的最小正周期是T==π.
由sin(2x-)=0得2x-=kπ,∴x=+,
∴函数f(x)的图象的对称中心是(+,1)(其中k∈Z).
(2)当x∈[,]时,
2x-∈[,],
sin(2x-)∈[,1],
4sin(2x-)+1∈[3,5],
故函数f(x)在区间[,]上的值域是[3,5]
=4sin2(x+)+4sin2x-(1+2)
=2[1-cos(2x+)]-2cos2x-1=4sin(2x-)+1.
(1)函数f(x)的最小正周期是T==π.
由sin(2x-)=0得2x-=kπ,∴x=+,
∴函数f(x)的图象的对称中心是(+,1)(其中k∈Z).
(2)当x∈[,]时,
2x-∈[,],
sin(2x-)∈[,1],
4sin(2x-)+1∈[3,5],
故函数f(x)在区间[,]上的值域是[3,5]
略

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 ,如
,如 .已知
.已知 ,
, ,则
,则
 ( )
( ) 



 <
< ,则函数y=
,则函数y= 的值域为
的值域为 )
) )
)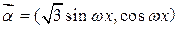 ,
, 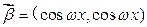 ,记函数
,记函数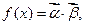 已知
已知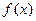 的周期为π.
的周期为π.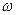 之值;
之值;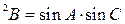 ,试求f(x)的值域.
,试求f(x)的值域.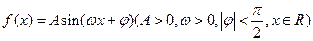 在一个周期内的图像如图所示
在一个周期内的图像如图所示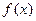 的
的 解析式;
解析式;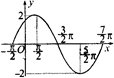
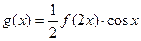 ,求,
,求,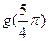 的值
的值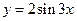 变为曲线
变为曲线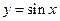 的伸缩变换 (设
的伸缩变换 (设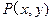 是曲线
是曲线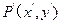 是曲线
是曲线



 ),由最高点运动到相邻的最低点时,曲线与
),由最高点运动到相邻的最低点时,曲线与 轴交点E的坐标为(6,0),求A、ω、j的值.
轴交点E的坐标为(6,0),求A、ω、j的值.