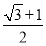题目内容
已知F1,F2分别为椭圆C1: =1(a>b>0)的上下焦点,其中F1是抛物线C2:x2=4y的焦点,点M是C1与C2在第二象限的交点,且|MF1|=
=1(a>b>0)的上下焦点,其中F1是抛物线C2:x2=4y的焦点,点M是C1与C2在第二象限的交点,且|MF1|= .
.

(1)试求椭圆C1的方程;
(2)与圆x2+(y+1)2=1相切的直线l:y=k(x+t)(t≠0)交椭圆于A,B两点,若椭圆上一点P满足 ,求实数λ的取值范围.
,求实数λ的取值范围.
(1)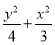 =1(2)(-2,0)∪(0,2)
=1(2)(-2,0)∪(0,2)
【解析】(1)由C2:x2=4y知F1(0,1),c=1,
设M(x0,y0)(x0<0),
因M在抛物线C2上,
故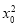 =4y0,①
=4y0,①
又|MF1|=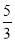 ,则y0+1=
,则y0+1=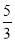 ②
②
由①②解得x0=-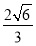 ,y0=
,y0=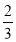 .
.
而点M在椭圆上,
∴2a=|MF1|+|MF2|=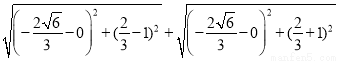 =4.
=4.
∴a=2,∴b2=a2-c2=3.
故椭圆C1的方程为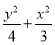 =1.
=1.
(2)因为直线l:y=k(x+t)与圆x2+(y+1)2=1相切,
所以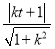 =1⇒k=
=1⇒k= (t≠0,k≠0).
(t≠0,k≠0).
把y=k(x+t)代入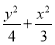 =1并整理,得
=1并整理,得
(4+3k2)x2+6k2tx+3k2t2-12=0,
设A(x1,y1),B(x2,y2),则有
x1+x2=-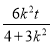 ,y1+y2=kx1+kt+kx2+kt=k(x1+x2)+2kt=
,y1+y2=kx1+kt+kx2+kt=k(x1+x2)+2kt=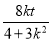 ,因为,λ
,因为,λ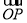 =(x1+x2,y1+y2)
=(x1+x2,y1+y2)
所以,P
又因为点P在椭圆上,
所以, +
+ =1⇒λ2=
=1⇒λ2=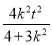 =
= (t≠0)
(t≠0)
因为t2>0,所以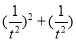 +1>1,
+1>1,
所以0<λ2<4,
当k=0时,因为直线l与圆x2+(y+1)2=1相切,
则t=0(舍去)或t=-1,
当t=-1时,
y=-1与椭圆有一个交点,不满足题意,
舍去.所以λ的取值范围是(-2,0)∪(0,2).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目