题目内容
已知函数f(x)=sin  +2cos2x-1(x∈R).
+2cos2x-1(x∈R).
(1)求函数f(x)的最小正周期及单调递增区间;
(2)在△ABC中,三内角A,B,C的对边分别为a,b,c,已知函数f(x)的图象经过点 ,b,a,c成等差数列,且
,b,a,c成等差数列,且 ·
·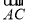 =9,求a的值.
=9,求a的值.
(1)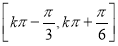 (k∈Z)(2)a=3
(k∈Z)(2)a=3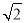
【解析】f(x)=sin 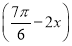 +2cos 2x-1=-
+2cos 2x-1=-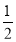 cos 2x+
cos 2x+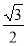 sin 2x+cos 2x=
sin 2x+cos 2x=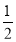 cos 2x+
cos 2x+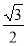 sin 2x=sin
sin 2x=sin 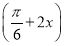 .
.
(1)最小正周期T=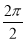 =π,由2kπ-
=π,由2kπ-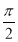 ≤2x+
≤2x+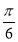 ≤2kπ+
≤2kπ+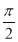 (k∈Z),得kπ-
(k∈Z),得kπ-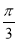 ≤x≤kπ+
≤x≤kπ+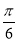 (k∈Z),所以f(x)的单调递增区间为
(k∈Z),所以f(x)的单调递增区间为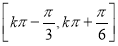 (k∈Z).
(k∈Z).
(2)由f(A)=sin 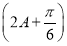 =
=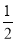 得2A+
得2A+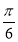 =
=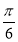 +2kπ或
+2kπ或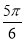 +2kπ(k∈Z),即A=kπ或A=
+2kπ(k∈Z),即A=kπ或A=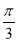 +kπ,又A为△ABC的内角,所以A=
+kπ,又A为△ABC的内角,所以A=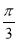 .
.
又因为b,a,c成等差数列,所以2a=b+c.
∵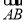 ·
·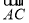 =bccos A=
=bccos A=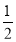 bc=9,∴bc=18,∴cos A=
bc=9,∴bc=18,∴cos A=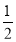 =
=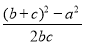 -1=
-1=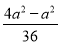 -1=
-1=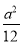 -1.∴a=3
-1.∴a=3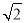

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
























