题目内容
20．已知等差数列{an}的前n项和为Sn，a5=5，S5=15．（1）求数列{an}的通项公式；
（2）求数列{2n•an}的前n项和Tn．
分析 （1）通过等差数列的求和公式S5=$\frac{5（{a}_{1}+{a}_{5}）}{2}$计算可知a1=1，进而可求出d=$\frac{{a}_{5}-{a}_{1}}{5-1}$，计算即得结论；
（2）通过（1）可知2n•an=n•2n，利用错位相减法计算即得结论．
解答 解：（1）依题意，S5=15=$\frac{5（{a}_{1}+{a}_{5}）}{2}$=$\frac{5（{a}_{1}+5）}{2}$，
解得：a1=1，d=$\frac{{a}_{5}-{a}_{1}}{5-1}$=$\frac{5-1}{5-1}$=1，
∴数列{an}是首项、公差均为1的等差数列，
∴数列{an}的通项公式an=n；
（2）由（1）可知2n•an=n•2n，
∴Tn=1•2+2•22+…+n•2n，2Tn=1•22+2•23+…+（n-1）•2n+n•2n+1，
错位相减得：-Tn=2+22+23+…+2n-n•2n+1，
∴Tn=n•2n+1-（2+22+23+…+2n）=n•2n+1-$\frac{2（1-{2}^{n}）}{1-2}$=2+（n-1）•2n+1．
点评 本题考查数列的通项及前n项和，考查运算求解能力，利用错位相减法是解决本题的关键，注意解题方法的积累，属于基础题．
练习册系列答案
相关题目
10．已知定义在R上的函数y=f（x）满足以下三个条件：
①对于任意的x∈R，都有f（x+4）=f（x）；
②对于任意的x1，x2∈R，且0≤x1＜x2≤2，都有f（x1）＜f（x2）；
③函数y=f（x+2）的图象关于y轴对称
则下列结论中正确的是（ ）
①对于任意的x∈R，都有f（x+4）=f（x）；
②对于任意的x1，x2∈R，且0≤x1＜x2≤2，都有f（x1）＜f（x2）；
③函数y=f（x+2）的图象关于y轴对称
则下列结论中正确的是（ ）
| A． | f （4.5）＜f （7）＜f （6.5） | B． | f （7）＜f （4.5）＜f （6.5） | C． | f （7）＜f （6.5）＜f （4.5） | D． | f （4.5）＜f （6.5）＜f （7） |
9．函数f（x）=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}x\\;x≥1}\\{{2}^{x}\\;x＜1}\end{array}\right.$的值域为（ ）
| A． | （-∞，0] | B． | （-∞，2） | C． | [0，+∞） | D． | （2，+∞） |
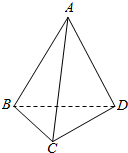如图，在四面体ABCD中，已知∠ABD=∠CBD=60°，AB=BC=2，