Question

20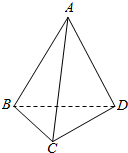．如图，在四面体ABCD中，已知∠ABD=∠CBD=60°，AB=BC=2，
（Ⅰ） 求证：AC⊥BD；
（Ⅱ）若平面ABD⊥平面CBD，且BD=$\frac{5}{2}$，求二面角C-AD-B的余弦值．

Answer 1

分析 （I）证明（方法一）：通过证明△ABD≌△CBD．得到AD=CD，取AC的中点E，连结BE、DE，证明BE⊥AC，DE⊥AC，然后证明AC⊥平面BED，推出AC⊥BD．
（方法二）：过C作CH⊥BD于点H．连接AH，证明AH⊥BD，然后证明BD⊥平面ACH，推出AC⊥BD．
（方法三）：通过证明AC与BD对应向量的数量积为0，证明二者垂直．
（II）过C作CH⊥BD于点H．证明CH⊥平面ABD．过H做HK⊥AD于点K，连接CK．说明CKH为二面角C-AD-B的平面角．连接AH．然后计算$tan∠CKH=\frac{CH}{HK}=\frac{{\sqrt{21}}}{3}$，即可求解二面角C-AD-B的余弦值．

解答 （本题14分）（I）证明（方法一）：∵∠ABD=∠CBD，AB=BC，BD=BD．
∴△ABD≌△CBD．∴AD=CD．…（2分）

取AC的中点E，连结BE、DE，则BE⊥AC，DE⊥AC，．
…（3分）
又∵BE∩DE=E，…（4分）
BE?平面BED，BD?平面BED，
∴AC⊥平面BED，…（6分）
∴AC⊥BD…（7分）
（方法二）：过C作CH⊥BD于点H．连接AH．…（1分）
∵∠ABD=∠CBD，AB=BC，BD=BD．
∴△ABD≌△CBD．∴AH⊥BD．…（3分）
又∵AH∩CH=H，…（4分），
AH?平面ACH，CH?平面ACH，
∴BD⊥平面ACH．…（6分）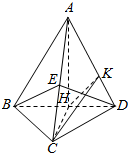

又∵AC?平面ACH，
∴AC⊥BD．…（7分）
（方法三）：$\overrightarrow{AC}•\overrightarrow{BD}=（\overrightarrow{BC}-\overrightarrow{BA}）•\overrightarrow{BD}$…（2分）
=$\overrightarrow{BC}•\overrightarrow{BD}-\overrightarrow{BA}•\overrightarrow{BD}$…（3分）
=$|{\overrightarrow{BC}}|•|{\overrightarrow{BD}}|cos∠CBD-\overrightarrow{|{BA}|}•|{\overrightarrow{BD}}|cos∠ABD$…（4分）
=2BDcos60°-2BDcos60°=0，…（6分）
∴AC⊥BD．…（7分）
（II）解：
过C作CH⊥BD于点H．则CH?平面BCD，
又∵平面ABD⊥平面BCD，平面ABD∩平面BCD=BD，
∴CH⊥平面ABD．
过H做HK⊥AD于点K，连接CK．
∵CH⊥平面ABD，∴CH⊥AD，又HK∩CH=H，
∴AD⊥平面CHK，∴CK⊥AD．
∴∠CKH为二面角C-AD-B的平面角．
连接AH．∵△ABD≌△CBD，∴AH⊥BD．
∵∠ABD=∠CBD=60°，AB=BC=2，
∴$AH=CH=\sqrt{3}$，BH=1．∵$BD=\frac{5}{2}$，∴$DH=\frac{3}{2}$．
∴$AD=\frac{{\sqrt{21}}}{2}$∴$HK=\frac{AH•DH}{AD}=\frac{{3\sqrt{7}}}{7}$．
∴$tan∠CKH=\frac{CH}{HK}=\frac{{\sqrt{21}}}{3}$，∴$cos∠CKH=\frac{{\sqrt{30}}}{10}$．
∴二面角C-AD-B的余弦值为$\frac{{\sqrt{30}}}{10}$．…（14分）

点评 本题考查二面角的平面角的求法，直线与平面垂直的判定定理以及性质定理的应用，考查逻辑推理能力以及空间想象能力．