题目内容
16.以下四个命题.:①若$\underset{lim}{n→∞}$an存在,则$\underset{lim}{n→∞}$an2也存在;
②若$\underset{lim}{n→∞}$|an|存在,则$\underset{lim}{n→∞}$an也存在;
③若$\underset{lim}{n→∞}$an存在,则$\underset{lim}{n→∞}$$\frac{{a}_{n}}{{a}_{n}+1}$也存在.
④若$\underset{lim}{n→∞}$(an-bn),$\underset{lim}{n→∞}$(an+bn)存在,则$\underset{lim}{n→∞}$an与$\underset{lim}{n→∞}$bn都存在;
其中假命题的个数为 ( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 由数列的定义及极限的定义,举反例即可.
解答 解:①若$\underset{lim}{n→∞}$an存在,不妨设$\underset{lim}{n→∞}$an=A,则$\underset{lim}{n→∞}$an2=A2,故成立;
②不妨设an=(-1)n,故$\underset{lim}{n→∞}$|an|存在,$\underset{lim}{n→∞}$an不存在;
③若$\underset{lim}{n→∞}$an存在,不妨设$\underset{lim}{n→∞}$an=A,当A=-1时,$\underset{lim}{n→∞}$$\frac{{a}_{n}}{{a}_{n}+1}$不存在.
④若$\underset{lim}{n→∞}$(an-bn)=A,$\underset{lim}{n→∞}$(an+bn)=B,则$\underset{lim}{n→∞}$an=$\frac{A+B}{2}$,$\underset{lim}{n→∞}$bn=$\frac{B-A}{2}$;
故选:C.
点评 本题考查了极限的定义及数列的定义的应用.

练习册系列答案
相关题目
4.已知变量x,y满足:$\left\{\begin{array}{l}{2x-y≤0}\\{x-2y+3≥0}\\{x≥0}\end{array}\right.$,则z=($\sqrt{3}$)2x+y的最大值为( )
| A. | $\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 3 | D. | 9 |
11.已知函数y=f(x),x∈[1,2]的图象为一线段,若1<a<2,则f(a)等于( )
| A. | (a-1)f(1)+(2-a)f(2) | B. | (2-a)f(1)+(a-1)f(2) | C. | (2-a)f(1)+(1-a)f(2) | D. | (1-a)f(1)+(2-a)f(2) |
8.已知f(x)是奇函数,且在(0,+∞)上是增函数,若f(4)=0,则满足xf(x)≤0的x取值范围是( )
| A. | [-4,4] | B. | (-4,4) | C. | [-4,0)∪(0,4] | D. | (-∞,4)∪(4,+∞) |
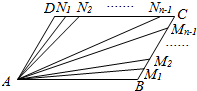 如图,已知平行四边形ABCD,点M1,M2,M3,…,Mn-1和N1,N2,N3,…,Nn-1分别将线段BC和DCn等分(n∈N*,n≥2),若$\overrightarrow{A{M}_{1}}$$+\overrightarrow{A{M}_{2}}$+…$+\overrightarrow{A{M}_{n-1}}$+$\overrightarrow{A{N}_{1}}$$+\overrightarrow{A{N}_{2}}$+…$+\overrightarrow{A{N}_{n-1}}$=30$\overrightarrow{AC}$,则n=( )
如图,已知平行四边形ABCD,点M1,M2,M3,…,Mn-1和N1,N2,N3,…,Nn-1分别将线段BC和DCn等分(n∈N*,n≥2),若$\overrightarrow{A{M}_{1}}$$+\overrightarrow{A{M}_{2}}$+…$+\overrightarrow{A{M}_{n-1}}$+$\overrightarrow{A{N}_{1}}$$+\overrightarrow{A{N}_{2}}$+…$+\overrightarrow{A{N}_{n-1}}$=30$\overrightarrow{AC}$,则n=( )