题目内容

8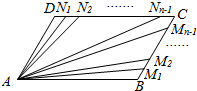．如图，已知平行四边形ABCD，点M1，M2，M3，…，Mn-1和N1，N2，N3，…，Nn-1分别将线段BC和DCn等分（n∈N*，n≥2），若$\overrightarrow{A{M}_{1}}$$+\overrightarrow{A{M}_{2}}$+…$+\overrightarrow{A{M}_{n-1}}$+$\overrightarrow{A{N}_{1}}$$+\overrightarrow{A{N}_{2}}$+…$+\overrightarrow{A{N}_{n-1}}$=30$\overrightarrow{AC}$，则n=（　　）
A．20B．21C．22D．23

分析 如图所示，利用向量的三角形法则可得：$\overrightarrow{A{M}_{n-1}}$=$\overrightarrow{AB}$+$\frac{n-1}{n}$$\overrightarrow{BC}$，$\overrightarrow{A{N}_{n-1}}$=$\overrightarrow{AD}$+$\frac{n-1}{n}$$\overrightarrow{DC}$．相加即可得出答案．

解答 解：如图所示，
∵点M1，M2，M3，…，Mn-1和N1，N2，N3，…，Nn-1分别将线段BC和DC进行n等分，
∴$\overrightarrow{A{M}_{n-1}}$=$\overrightarrow{AB}$+$\frac{n-1}{n}$$\overrightarrow{BC}$，$\overrightarrow{A{N}_{n-1}}$=$\overrightarrow{AD}$+$\frac{n-1}{n}$$\overrightarrow{DC}$．
∴$\overrightarrow{A{M}_{1}}$$+\overrightarrow{A{M}_{2}}$+…$+\overrightarrow{A{M}_{n-1}}$+$\overrightarrow{A{N}_{1}}$$+\overrightarrow{A{N}_{2}}$+…$+\overrightarrow{A{N}_{n-1}}$=n（$\overrightarrow{AB}$+$\overrightarrow{AD}$）+（$\frac{1}{n}$+$\frac{2}{n}$+…+$\frac{n-1}{n}$）（$\overrightarrow{BC}$+$\overrightarrow{DC}$）
=n（$\overrightarrow{AB}$+$\overrightarrow{AD}$）+（$\frac{1}{n}$+$\frac{2}{n}$+…+$\frac{n-1}{n}$）（$\overrightarrow{AB}$+$\overrightarrow{AD}$）
=$\frac{3（n-1）}{2}$（$\overrightarrow{AB}$+$\overrightarrow{AD}$）
=$\frac{3（n-1）}{2}$$\overrightarrow{AC}$=30$\overrightarrow{AC}$，
解得n=21．
故选：B．

点评 本题考查了向量的三角形法则、等差数列的前n项和公式、向量的平行四边形法则，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
18．函数f（x）=$\frac{ax+2015b}{{x}^{2}+1}$是定义在（-∞，+∞）上的奇函数，且f（$\frac{1}{3}$）=$\frac{3}{10}$．
（1）求实数a，b，并确定函数f（x）的解析式；
（2）用定义证明f（x）在（-1，1）上是增函数；
（3）写出f（x）的单调减区间，并判断f（x）有无最大值或最小值？如有，写出最大值或最小值．（本小问不需说明理由）
19．“1，x，16成等比数列”是“x=4”成立的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
16．如图，三棱锥P-ABC中，PA=PB=PC=AC=4，AB=BC=2$\sqrt{2}$．
（1）求证：平面ABC⊥平面APC；
（2）求直线PA与平面PBC所成角的正弦值；
（3）若M为棱BC上一点，且二面角M-PA-C的大小为$\frac{π}{6}$，求$\frac{BM}{BC}$的值．
3．在平面直角坐标系xOy中，直线l的参数方程是$\left\{\begin{array}{l}{x=t}\\{y=3t+a}\end{array}\right.$，以O为极点，x轴非负半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ=2$\sqrt{2}$cos（θ+$\frac{π}{4}$）．
（1）求曲线C的直角坐标方程；
（2）若直线l过点（2，3），求直线l被圆C截得的弦长．
13．如图，直四棱柱ABCD-A1B1C1D1中，AB∥CD，AD⊥AB，AB=2，AD=$\sqrt{2}$，AA1=3，E为CD上一点，DE=1，EC=3．
（1）求BE和BC的长；
（2）证明：BE⊥平面BB1C1C．
20．如图所示，将长方形OBCD沿对角线OC折叠，OD=8，OB=4，求E点坐标．
15．若0＜x1＜x2，0＜y1＜y2，且x1+x2=y1+y2=1，则下列代数式中值最大的是（　　）
A．x1y1+x2y2B．x1x2+y1y2C．x1y2+x2y1D．$\frac{1}{2}$
16．以下四个命题．：
①若$\underset{lim}{n→∞}$an存在，则$\underset{lim}{n→∞}$an2也存在；
②若$\underset{lim}{n→∞}$|an|存在，则$\underset{lim}{n→∞}$an也存在；
③若$\underset{lim}{n→∞}$an存在，则$\underset{lim}{n→∞}$$\frac{{a}_{n}}{{a}_{n}+1}$也存在．
④若$\underset{lim}{n→∞}$（an-bn），$\underset{lim}{n→∞}$（an+bn）存在，则$\underset{lim}{n→∞}$an与$\underset{lim}{n→∞}$bn都存在；
其中假命题的个数为 （　　）
A．4B．3C．2D．1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网