��Ŀ����
����Ŀ�� ij��ѧ�Ļ������Ų��չ��һ������ƶ��˸�У���������������ָ������������ȼ���Ӧ��ϵ���±�������������������ָ�����ᳬ��300����
��������ָ�� |
|
|
|
|
|
|
���������ȼ� |
|
|
��Ⱦ |
��Ⱦ |
��Ⱦ |
|
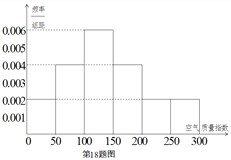
�����Ž���У����2016��100��Ŀ�������ָ�����������Ϊ���������Ƶ�Ƶ�ʷֲ�ֱ��ͼ����ͼ���Ѹ�ֱ��ͼ����Ƶ�ʹ���Ϊ������
�����������2017�꣨��365����㣩ȫ�������������������(δ��һ�찴һ�����)��
�������÷ֲ�����ķ�������ȡ10�죬���������ָ���ڣ�0��50]��(50��100]��(100��150]�������и�Ӧ��ȡ���죿
��������֪���������ȼ�Ϊ1��ʱ����Ҫ�������������������ȼ�Ϊ2��ʱÿ���辻�������ķ���Ϊ2000Ԫ�����������ȼ�Ϊ3��ʱÿ���辻�������ķ���Ϊ4000Ԫ�������������������£��ӿ�������ָ����![]() �������������ȡ��������������ľ��������ܷ���Ϊ4000Ԫ�ĸ�����
�������������ȡ��������������ľ��������ܷ���Ϊ4000Ԫ�ĸ�����
���𰸡�������110����������Ӧ��ȡ1��2��3���������� ![]() ��
��
���������������������������ֱ��ͼ�ɵù���2017�꣨��365����㣩ȫ���������������Ƶ�ʣ��Ӷ��ɵý��������������ÿ�������ָ���ڣ�0��50]��(50��100]��(100��150]�������ı������Ӷ����ݷֲ���������ɵý�������������оٳ���������ָ���� �������������ȡ���칲��![]() �֣����������Ĺ���
�֣����������Ĺ���![]() �֣����ݹŵ�����ʹ�ʽ�ɵý��.
�֣����ݹŵ�����ʹ�ʽ�ɵý��.
�����������������ֱ��ͼ�ɹ���2017�꣨��365����㣩ȫ�������������������Ϊ
![]() ���죩��
���죩��
��������������ָ���ڣ�0��50]��(50��100]��(100��150]�������и�Ӧ
��ȡ1��2��3����
�������������ָ���ڣ�0��50]��һ��ΪA����������ָ���ڣ�50��100]������Ϊb��c��
��������ָ���ڣ�100��150]������Ϊ1��2��3����������������ȡ��������п��ܽ��Ϊ��Ab������Ac������A1������A2������A3������bc������b1������b2������b3������c1������c2������c3������12������13������23��.��15��.
����������ľ��������ܷ���Ϊ4000Ԫ�Ŀ��ܽ��Ϊ��A1������A2������A3������bc��.
P(������ľ��������ܷ���Ϊ4000Ԫ)= ![]() .
.

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�