题目内容
【题目】某单位有老年人30人,中年人90人,青年人60人,为了调查他们的身体健康状况,采用分层抽样的方法从他们中间抽取一个容量为36的样本,则应抽取老年人的人数是( )
A.5
B.6
C.7
D.8
【答案】B
【解析】解:某单位有老年人30人,中年人90人,青年人60人,这个单位共有30+90+60=180,假设用分层抽样的方法从他们中抽取了36个人进行体检,
则每个个体被抽到的概率是 ![]() =
= ![]()
∴应抽取老年人的人数是30× ![]() =6,
=6,
故选:6.
【考点精析】通过灵活运用分层抽样,掌握先将总体中的所有单位按照某种特征或标志(性别、年龄等)划分成若干类型或层次,然后再在各个类型或层次中采用简单随机抽样或系用抽样的办法抽取一个子样本,最后,将这些子样本合起来构成总体的样本即可以解答此题.

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案【题目】 某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):
空气质量指数 |
|
|
|
|
|
|
空气质量等级 |
|
|
污染 |
污染 |
污染 |
|
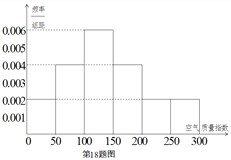
该社团将该校区在2016年100天的空气质量指数监测数据作为样本,绘制的频率分布直方图如下图,把该直方图所得频率估计为概率.
(Ⅰ)请估算2017年(以365天计算)全年空气质量优良的天数(未满一天按一天计算);
(Ⅱ)用分层抽样的方法共抽取10天,则空气质量指数在(0,50],(50,100],(100,150]的天数中各应抽取几天?
(Ⅲ)已知空气质量等级为1级时不需要净化空气,空气质量等级为2级时每天需净化空气的费用为2000元,空气质量等级为3级时每天需净化空气的费用为4000元.若在(Ⅱ)的条件下,从空气质量指数在![]() 的天数中任意抽取两天,求这两天的净化空气总费用为4000元的概率.
的天数中任意抽取两天,求这两天的净化空气总费用为4000元的概率.