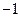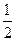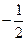题目内容
证明:三角形重心与顶点的距离等于它到对边中点的距离的两倍.
设 = b,
= b,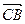 = a,则
= a,则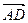 =
= +
+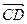 = b+
= b+ a,
a, 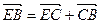 =
= b+a
b+a
∵A, G, D共线,B, G, E共线
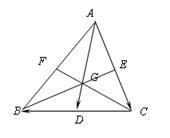
∴可设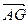 =λ
=λ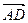 ,
,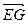 = μ
= μ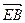 ,
,
则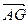 =λ
=λ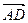 =λ(b+
=λ(b+ a)=λb+
a)=λb+ λa,
λa,
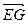 = μ
= μ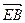 = μ(
= μ( b+ a)=
b+ a)= μb+μa,
μb+μa,
∵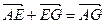 即:
即: b + (
b + ( μb+μa) =λb+
μb+μa) =λb+ λa
λa
∴(μ- λ) a + (
λ) a + ( μ-λ+
μ-λ+ )b =" 0 " ∵a, b不平行,
)b =" 0 " ∵a, b不平行,
∴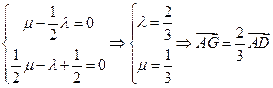
 = b,
= b,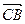 = a,则
= a,则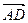 =
= +
+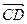 = b+
= b+ a,
a, 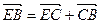 =
= b+a
b+a∵A, G, D共线,B, G, E共线

∴可设
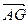 =λ
=λ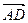 ,
,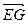 = μ
= μ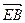 ,
,则
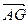 =λ
=λ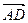 =λ(b+
=λ(b+ a)=λb+
a)=λb+ λa,
λa,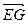 = μ
= μ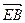 = μ(
= μ( b+ a)=
b+ a)= μb+μa,
μb+μa,∵
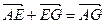 即:
即: b + (
b + ( μb+μa) =λb+
μb+μa) =λb+ λa
λa∴(μ-
 λ) a + (
λ) a + ( μ-λ+
μ-λ+ )b =" 0 " ∵a, b不平行,
)b =" 0 " ∵a, b不平行,∴
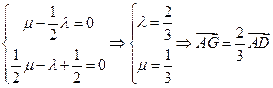

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案
相关题目
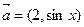 ,
,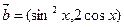 ,函数
,函数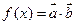 . (Ⅰ)求
. (Ⅰ)求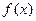 的单调增区间; (II)若在
的单调增区间; (II)若在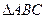 中,角
中,角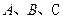 所对的边分别是
所对的边分别是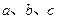 ,且满足:
,且满足: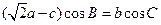 ,求
,求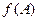 的取值范围.
的取值范围.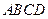 的一个顶点至
的一个顶点至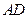 、
、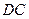 边的中点
边的中点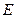 、
、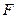 ,
,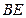 、
、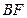 分别与
分别与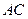 交于
交于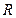 、
、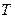 两点,你能发现
两点,你能发现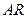 、
、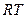 、
、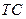 之间的关系吗?
之间的关系吗?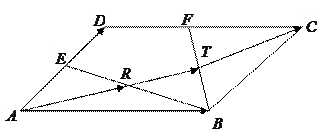

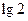 ,
,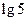 ,
,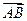 的坐标.
的坐标.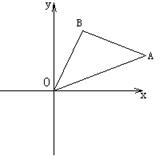
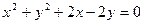 按向量
按向量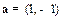 平移得到圆
平移得到圆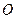 ,直线
,直线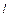 与圆
与圆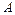 、
、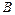 两点,若在圆
两点,若在圆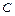 ,使
,使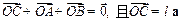 .求直线
.求直线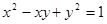 有以下判断:(1)它表示圆;(2)它关于原点对称;(3)它关于直线
有以下判断:(1)它表示圆;(2)它关于原点对称;(3)它关于直线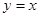 对称;(4)
对称;(4)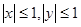 .其中正确的有________(填上相应的序号即可).
.其中正确的有________(填上相应的序号即可).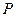 是
是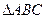 的外心,且
的外心,且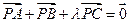 ,
,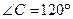 ,则实数
,则实数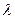 的值为( )
的值为( )