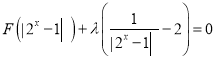题目内容
【题目】已知函数![]() ,
, ![]() 为常数.
为常数.
(![]() )若
)若![]() ,求
,求![]() 的取值范围.
的取值范围.
(![]() )若对任意的
)若对任意的![]() 都有不等式
都有不等式![]() 成立,求
成立,求![]() 的值.
的值.
(![]() )在(
)在(![]() )的条件下,若函数
)的条件下,若函数![]() 的图像与
的图像与![]() 轴恰有三个相异的公共点,求实数
轴恰有三个相异的公共点,求实数![]() 的取值范围.
的取值范围.
【答案】(![]() )
)![]() ;(
;(![]() )
)![]() ;(
;(![]() )
)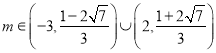 .
.
【解析】试题分析:(1)对二次项系数进行讨论,分为![]() 符合题意,
符合题意, ![]() 时,根据为此函数的性质可得不合题意,
时,根据为此函数的性质可得不合题意, ![]() 时,解一元二次不等式可得结果;(2)根据一元二次不等式的性质可得
时,解一元二次不等式可得结果;(2)根据一元二次不等式的性质可得![]() 时,不合题意,故应
时,不合题意,故应![]() ,
, ![]() ,从而可解出
,从而可解出![]() ;(3)结合(2)中的结果将其利用分段函数进行表达
;(3)结合(2)中的结果将其利用分段函数进行表达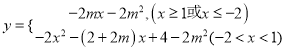 ,根据一次函数的性质可得
,根据一次函数的性质可得![]() 必有一根,解出方程得
必有一根,解出方程得![]() ,根据二次函数的性质可得
,根据二次函数的性质可得![]() 必有两个不等根,利用数形结合思想得
必有两个不等根,利用数形结合思想得![]() ,综合可得最后结果.
,综合可得最后结果.
试题解析:(![]() )当
)当![]() 时,
时, ![]() 时,
时, ![]() ,符合;
,符合;
当![]() 时,开口向下,在
时,开口向下,在![]() 上不能恒正,舍;
上不能恒正,舍;
当![]() 时,
时, ![]() ,
,
解得: ![]() 或
或![]() ,符合;综上:
,符合;综上: ![]() 的范围是
的范围是![]() .
.
(![]() )
)![]() ,
, ![]() ,对
,对![]() 恒成立,
恒成立,
当![]() 时,
时, ![]() ,不合题意(舍);当
,不合题意(舍);当![]() 时,不合题意(舍);当
时,不合题意(舍);当![]() 时,
时, ![]() ,即
,即![]() ,∴综上:
,∴综上: ![]() .
.
(![]() )
)![]() ,
,
∴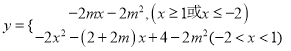 ,
,
则![]() ,必有一根,
,必有一根, ![]() ,
, ![]() 或
或![]() ,
,
![]() ,必有两个不等根,
,必有两个不等根,
∴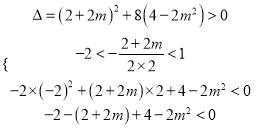 ,得
,得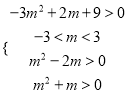 ,
,
综上: ![]() 范围
范围 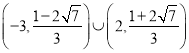 .
.

练习册系列答案
相关题目