题目内容
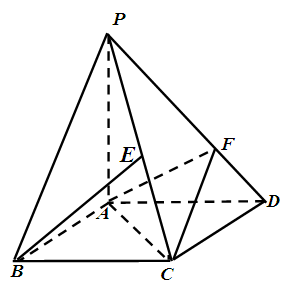
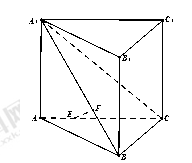
如图,四棱锥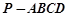 的底面ABCD是平行四边形,
的底面ABCD是平行四边形,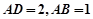 ,
,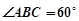 ,
,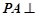 面
面 ,设
,设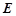 为
为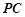 中点,点
中点,点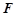 在线段
在线段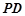 上且
上且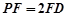 .
.
(1)求证: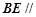 平面
平面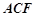 ;
;
(2)设二面角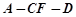 的大小为
的大小为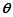 ,若
,若 ,求
,求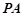 的长.
的长.
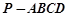 的底面ABCD是平行四边形,
的底面ABCD是平行四边形,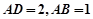 ,
,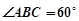 ,
,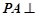 面
面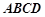 ,设
,设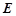 为
为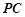 中点,点
中点,点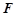 在线段
在线段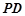 上且
上且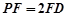 .
.
(1)求证:
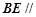 平面
平面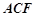 ;
;(2)设二面角
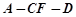 的大小为
的大小为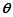 ,若
,若 ,求
,求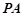 的长.
的长.( 1 )证明过程详见解析;(2) 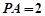 .
.
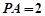 .
.试题分析:
(1)利用三角形的余弦定理和勾股定理即可证明
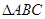 为直角三角形,即
为直角三角形,即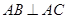 .再根据垂直的判断可以得到
.再根据垂直的判断可以得到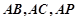 相互垂直,即可以以这三条边建立三维空间直角坐标系,利用坐标法来证明线面平行,首先求出平面ACF的法向量,计算法向量与BE的内积,证明该内积为0即可得到线面平行.
相互垂直,即可以以这三条边建立三维空间直角坐标系,利用坐标法来证明线面平行,首先求出平面ACF的法向量,计算法向量与BE的内积,证明该内积为0即可得到线面平行.(2)利用第(1)问平面ACF的法向量,再求出面DCF的法向量,则二面角即为两法向量所成角或者其补角,故两法向量夹角的余弦值为满足
 ,即可求出PA的长度.
,即可求出PA的长度.试题解析:
(1)由
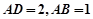 ,
,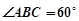 得
得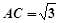 ,
,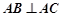 .
.又
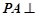 面
面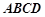 ,所以以
,所以以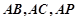 分别为
分别为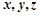 轴建立坐标系如图.
轴建立坐标系如图.则
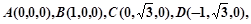
设
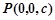 ,则
,则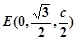 .
.设
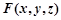 ,
,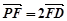 得:
得: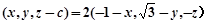 .
.解得:
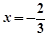 ,
,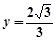 ,
,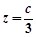 ,
,所以
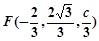 . 5分
. 5分所以
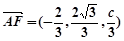 ,
,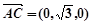 ,
,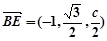 .
.设面
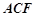 的法向量为
的法向量为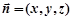 ,则
,则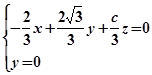 ,取
,取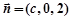 .
.因为
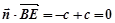 ,且
,且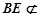 面
面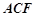 ,所以
,所以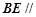 平面
平面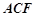 . 9分
. 9分

(2)设面
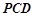 法向量为
法向量为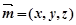 , 因为
, 因为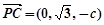 ,
,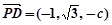 ,
,所以
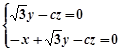 ,取
,取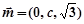 . 11分
. 11分由
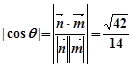 ,得
,得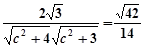 .
.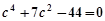 ,
,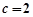 ,所以
,所以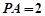 . 15分
. 15分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,
中,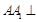 底面
底面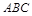 ,
,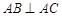 ,
,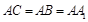 ,
,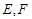 分别是棱
分别是棱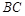 ,
,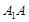 的中点,
的中点,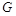 为棱
为棱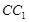 上的一点,且
上的一点,且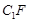 //平面
//平面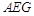 .
.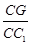 的值;
的值;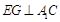 ;
; 的余弦值.
的余弦值.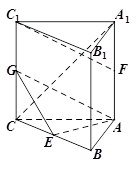
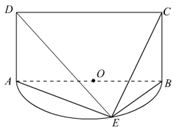
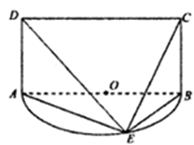
 是以
是以 为直径的半圆
为直径的半圆 上异于
上异于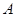 、
、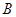 的点,矩形
的点,矩形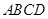 所在的平面垂直于半圆
所在的平面垂直于半圆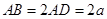 .
.
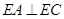 ;
;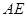 和
和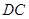 所成的角为
所成的角为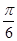 ,求平面
,求平面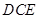 与平面
与平面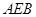 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.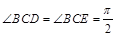 ,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.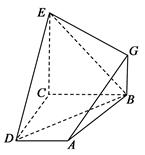
 平面BDE;
平面BDE; DE
DE 是以
是以 为直径的半圆
为直径的半圆 上异于
上异于 的点,矩形
的点,矩形 所在的平面垂直于半圆
所在的平面垂直于半圆 。
。
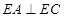 。
。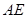 和
和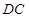 所成的角为
所成的角为 ,求平面
,求平面 和平面
和平面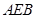 所成的锐二面角的余弦值。
所成的锐二面角的余弦值。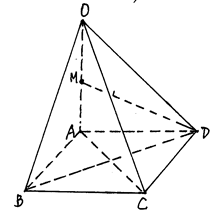
 (侧棱和底面垂直的棱柱)中,
(侧棱和底面垂直的棱柱)中, ,
, ,
,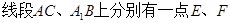 ,且满足
,且满足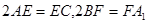 .
.
 侧面
侧面 ;
; 的平面角的余弦值。
的平面角的余弦值。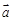 =(2, –2, 1), 已知P(-1, 3, 2),则P到平面OAB的距离等于 ( )
=(2, –2, 1), 已知P(-1, 3, 2),则P到平面OAB的距离等于 ( )