题目内容
【题目】求下列椭圆的标准方程:
(1)焦点在![]() 轴上,离心率
轴上,离心率![]() ,且经过点
,且经过点 ;
;
(2)以坐标轴为对称轴,且长轴长是短轴长的![]() 倍,并且过点
倍,并且过点![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)由焦点在![]() 轴上,可设椭圆的标准方程为
轴上,可设椭圆的标准方程为![]() ,将点A代入方程,由离心率与椭圆的系数关系整理得方程,由上述两个方程解得
,将点A代入方程,由离心率与椭圆的系数关系整理得方程,由上述两个方程解得![]() ,代入所设方程得答案;
,代入所设方程得答案;
(2)分类讨论焦点在![]() 轴与
轴与![]() 轴,利用待定系数法设出方程,代入点坐标可得方程,由已知长轴长是短轴长的
轴,利用待定系数法设出方程,代入点坐标可得方程,由已知长轴长是短轴长的![]() 倍又可构建方程,联立方程组求得所设方程系数,既得答案.
倍又可构建方程,联立方程组求得所设方程系数,既得答案.
(1)因为焦点在![]() 轴上,即设椭圆的标准方程为
轴上,即设椭圆的标准方程为![]() ,
,
∵椭圆经过点 ,
,![]() .①,
.①,
由已知![]() ,即
,即![]() .②,
.②,
把②代入①,得![]() ,解得
,解得![]() ,
,
∴椭圆的标准方程为![]() .
.
(2)若焦点在![]() 轴上,设方程为
轴上,设方程为![]()
因为椭圆过点![]() ,所以
,所以![]() ,又
,又![]() ,
,![]()
椭圆的标准方程为![]() ,
,
若焦点在![]() 轴上,设方程为
轴上,设方程为![]() 因为椭圆过点
因为椭圆过点![]() ,,所以
,,所以![]() ,又
,又![]() ,
,![]() ∴椭圆的方程为
∴椭圆的方程为![]()
综上,所求的椭圆方程是 ![]() 或
或![]()

练习册系列答案
相关题目
【题目】空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如表:
AQI指数值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 |
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
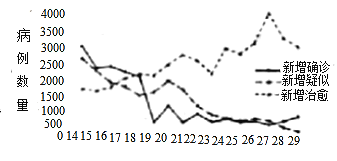
如图是某市12月1日-20日AQI指数变化趋势:

下列叙述正确的是( )
A.这20天中AQI指数值的中位数略高于100
B.这20天中的中度污染及以上的天数占![]()
C.该市12月的前半个月的空气质量越来越好
D.总体来说,该市12月上旬的空气质量比中旬的空气质量好