题目内容
【题目】已知椭圆![]() 的右顶点为
的右顶点为![]() ,
,![]() 为上顶点,点
为上顶点,点![]() 为椭圆
为椭圆![]() 上一动点.
上一动点.
(1)若![]() ,求直线
,求直线![]() 与
与![]() 轴的交点坐标;
轴的交点坐标;
(2)设![]() 为椭圆
为椭圆![]() 的右焦点,过点
的右焦点,过点![]() 与
与![]() 轴垂直的直线为
轴垂直的直线为![]() ,
,![]() 的中点为
的中点为![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,求证:直线
,求证:直线![]() 与直线
与直线![]() 的交点在椭圆
的交点在椭圆![]() 上.
上.
【答案】(1)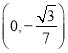 (2)见解析
(2)见解析
【解析】
(1)直接求出直线![]() 方程,与椭圆方程联立求出
方程,与椭圆方程联立求出![]() 点坐标,从而可得直线
点坐标,从而可得直线![]() 方程,得其与
方程,得其与![]() 轴交点坐标;
轴交点坐标;
(2)设![]() ,则
,则![]() ,求出直线
,求出直线![]() 和
和![]() 的方程,从而求得两直线的交点坐标,证明此交点在椭圆上,即此点坐标适合椭圆方程.代入验证即可.注意分
的方程,从而求得两直线的交点坐标,证明此交点在椭圆上,即此点坐标适合椭圆方程.代入验证即可.注意分![]() 和
和![]() 说明.
说明.
解:本题考查直线与椭圆的位置关系的综合,
(1)由题知![]() ,
,![]() ,则
,则![]() .因为
.因为![]() ,所以
,所以![]() ,
,
则直线![]() 的方程为
的方程为![]() ,联立
,联立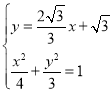 ,可得
,可得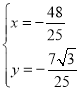
故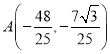 .则
.则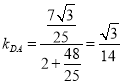 ,直线
,直线![]() 的方程为
的方程为![]() .令
.令![]() ,
,
得![]() ,故直线
,故直线![]() 与
与![]() 轴的交点坐标为
轴的交点坐标为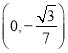 .
.
(2)证明:因为![]() ,
,![]() ,所以
,所以![]() .设点
.设点![]() ,则
,则![]() .
.
设
当![]() 时,设
时,设![]() ,则
,则![]() ,此时直线
,此时直线![]() 与
与![]() 轴垂直,
轴垂直,
其直线方程为![]() ,
,
直线![]() 的方程为
的方程为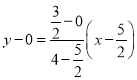 ,即
,即![]() .
.
在方程![]() 中,令
中,令![]() ,得
,得![]() ,得交点为
,得交点为![]() ,显然在椭圆
,显然在椭圆![]() 上.
上.
同理当![]() 时,交点也在椭圆
时,交点也在椭圆![]() 上.
上.
当![]() 时,可设直线
时,可设直线![]() 的方程为
的方程为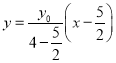 ,即
,即![]() .
.
直线![]() 的方程为
的方程为![]() ,联立方程
,联立方程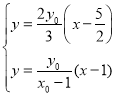 ,
,
消去![]() 得
得![]() ,化简并解得
,化简并解得![]() .
.
将![]() 代入
代入![]() 中,化简得
中,化简得![]() .
.
所以两直线的交点为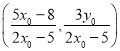 .
.
因为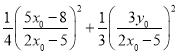
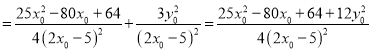 ,
,
又因为![]() ,所以
,所以![]() ,
,
则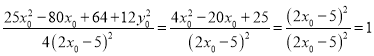 ,
,
所以点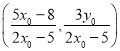 在椭圆
在椭圆![]() 上.
上.
综上所述,直线![]() 与直线
与直线![]() 的交点在椭圆
的交点在椭圆![]() 上.
上.

练习册系列答案
相关题目