题目内容
【题目】设![]() 四点均在双曲线
四点均在双曲线![]() 的右支上.
的右支上.
(1)若![]() (实数
(实数![]() ),证明:
),证明:![]() (O是坐标原点);
(O是坐标原点);
(2)若![]() ,P是线段AB的中点,过点P分别作该双曲线的两条渐近线的垂线,垂足为M、N,求四边形
,P是线段AB的中点,过点P分别作该双曲线的两条渐近线的垂线,垂足为M、N,求四边形![]() 的面积的最大值.
的面积的最大值.
【答案】(1)见解析(2)1
【解析】
(1)由![]() ,得
,得![]()
![]() 当直线AB的倾斜角为90°时,设其方程为
当直线AB的倾斜角为90°时,设其方程为![]() 设
设![]() ,则
,则![]() ,且点
,且点![]() 满足
满足![]()
![]() 同理
同理![]() =1,则
=1,则![]() .
.
![]() 设直线AB的方程为
设直线AB的方程为![]()
联立方程得![]() 整理为
整理为
![]() ①
①
故![]() ②
②
![]() ③
③
则![]()
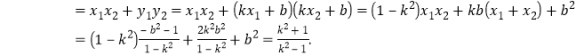 由
由![]() ,知直线AB与直线CD的斜率相等.同理,
,知直线AB与直线CD的斜率相等.同理,![]()
![]() 所以,
所以,![]() .
.
(2)由![]() ,平方得
,平方得![]()
将式②、③代入得![]() ④
④
由![]() ,知
,知![]() ,而
,而![]() 使方程①的判别式
使方程①的判别式![]() 成立.设
成立.设![]() 于是,
于是,
![]() , ⑤
, ⑤
![]() . ⑥
. ⑥
因为双曲线![]() 的两条渐近线相互垂直,所以,四边形
的两条渐近线相互垂直,所以,四边形![]() 是矩形,其面积S等于点P到渐近线
是矩形,其面积S等于点P到渐近线![]() 距离的乘积.于是,
距离的乘积.于是,![]() 将式⑤、⑥代入上式得
将式⑤、⑥代入上式得![]() 由式④得
由式④得![]() 又
又![]() ,则
,则![]() ,即直线AB的斜率存在时,所求四边形
,即直线AB的斜率存在时,所求四边形![]() 的面积
的面积![]()
当直线AB斜率不存在时,由![]() ,知点
,知点![]() ,则四边形
,则四边形![]() 的面积
的面积![]()
综上,四边形![]() 面积的最大值为1.
面积的最大值为1.

练习册系列答案
相关题目