题目内容
已知等差数列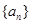 的首项
的首项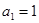 ,公差
,公差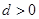 ,且第2项、第5项、第14项分别是等比数列
,且第2项、第5项、第14项分别是等比数列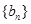 的第2项、第3项、第4项.
的第2项、第3项、第4项.
(1)求数列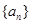 、
、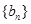 的通项公式;
的通项公式;
(2)设数列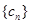 对任意的
对任意的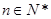 ,均有
,均有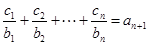 成立,求
成立,求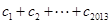 .
.
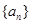 的首项
的首项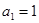 ,公差
,公差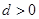 ,且第2项、第5项、第14项分别是等比数列
,且第2项、第5项、第14项分别是等比数列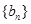 的第2项、第3项、第4项.
的第2项、第3项、第4项.(1)求数列
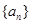 、
、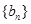 的通项公式;
的通项公式;(2)设数列
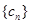 对任意的
对任意的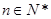 ,均有
,均有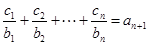 成立,求
成立,求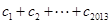 .
.(1)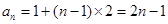 ,
,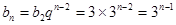 (2)
(2)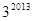 .
.
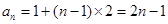 ,
,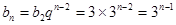 (2)
(2)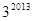 .
.试题分析:(1)由已知得
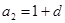 ,
,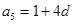 ,
,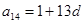 ,
,所以
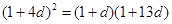 ,解得
,解得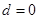 或
或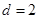 .
.又因为
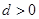 ,所以
,所以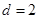 .所以
.所以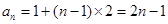 .
.又
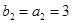 ,
,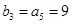 ,所以等比数列
,所以等比数列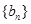 的公比
的公比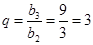 ,
,所以
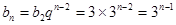 .
.(2)由
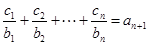 ①,得当
①,得当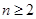 时,
时,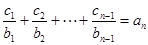 ②,
②,①-②,得当
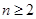 时,
时,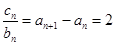 ,所以
,所以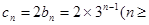 2).
2).而
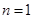 时,
时,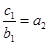 ,所以
,所以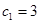 .所以
.所以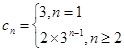 .
.所以
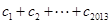
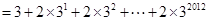
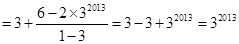 .
.点评:本题考查了等比数列的性质,以及等差数列和等比数列的通项公式的求法,对于复杂数列的前n项和求法我们一般先求出数列的通项公式,再依据数列的特点采取具体的方法.

练习册系列答案
相关题目
 中,
中,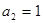 ,
,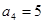 ,则
,则 =
=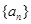 中,
中, 
 则
则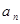 = .
= . 的前n项和为
的前n项和为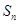 ,且
,且 ,则
,则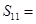 。
。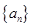 中,对于任意
中,对于任意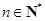 ,等式:
,等式: 恒成立,其中常数
恒成立,其中常数 .
.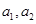 的值;
的值; 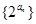 为等比数列;
为等比数列; 的不等式
的不等式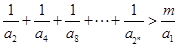 的解集为
的解集为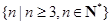 ,试求实数
,试求实数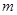 的取值范围.
的取值范围. ,且Sn的最大值为8,则a2= .
,且Sn的最大值为8,则a2= . 中,若
中,若 ,则
,则 ”为真命题,由于印刷问题,括号处的数模糊不清,可算得括号内的数为 .
”为真命题,由于印刷问题,括号处的数模糊不清,可算得括号内的数为 . 满足
满足 ,
, ,则
,则 。
。 首项为1,且
首项为1,且 成等比数列,
成等比数列,
 通项公式;
通项公式; 前n项和
前n项和 ;
; 成立,求
成立,求 范围.
范围.