题目内容
11. 如图,已知E,F分别是正方形ABCD边BC,CD的中点,EF与AC交于点O,PA,NC都垂直于平面ABCD,且PA=AB=2NC,M是PA中点.
如图,已知E,F分别是正方形ABCD边BC,CD的中点,EF与AC交于点O,PA,NC都垂直于平面ABCD,且PA=AB=2NC,M是PA中点.(Ⅰ)求证:平面PAC⊥平面NEF;
(Ⅱ)求二面角M-EF-N的余弦值.
分析 (Ⅰ)连结BD,利用线面垂直的判定定理及中位线定理即可;
(Ⅱ)连OM,建立空间直角坐标系,所求值即为平面NEF的一个法向量与平面MEF一个法向量的夹角的余弦值的绝对值,计算即可.
解答  解法1:(Ⅰ)连结BD,
解法1:(Ⅰ)连结BD,
∵PA⊥平面ABCD,BD?平面ABCD,∴PA⊥BD,
又∵BD⊥AC,AC⊥PA=A,∴BD⊥平面PAC,
又∵E,F分别是BC、BD的中点,∴EF∥BD,
∴EF⊥平面PAC,又EF⊆平面NEF,
∴平面PAC⊥平面NEF;
(Ⅱ)设AB=4,建立如图所示的直角坐标系,
则P(0,0,4),C(4,4,0),E(4,2,0),
F(2,4,0),M(0,0,2),N(4,4,2),
∴$\overrightarrow{PC}=(4,4,-4)$,$\overrightarrow{EF}=(-2,2,0)$,
则$\overrightarrow{EN}=(0,2,2)$,$\overrightarrow{EN}$=(0,2,2),
设平面NEF的法向量为$\overrightarrow m=(x,y,z)$,
则$\left\{\begin{array}{l}\overrightarrow m•\overrightarrow{EN}=0\\ \overrightarrow m•\overrightarrow{EF}=0\end{array}\right.⇒\left\{\begin{array}{l}2y+2z=0\\-2x+2y=0\end{array}\right.$,
令x=1,得y=1,z=-1,
即$\overrightarrow m=(1,1,-1)$,
同理可求平面MEF一个法向量$\overrightarrow n=(1,1,3)$,
∴$cos<\overrightarrow m,\overrightarrow n>=\frac{1+1-3}{{\sqrt{3}×\sqrt{11}}}=-\frac{{\sqrt{33}}}{33}$,
∴二面角M-EF-N的余弦值为$\frac{\sqrt{33}}{33}$.
点评 本题考查线面垂直、面面垂直的判定定理,考查求二面角,涉及到向量数量积运算,注意解题方法的积累,属于中档题.

| A. | -1 | B. | -2 | C. | -3 | D. | 1 |
| A. | 240种 | B. | 204种 | C. | 188种 | D. | 96种 |
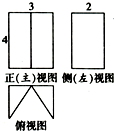
| A. | 24 | B. | 18 | C. | 16 | D. | 12 |
