题目内容
1．已知圆锥曲线mx2+y2=1的离心率为$\sqrt{2}$，则实数m的值为（ ）| A． | -1 | B． | -2 | C． | -3 | D． | 1 |
分析 由双曲线mx2+y2=1，化为标准方程，利用离心率e=$\sqrt{2}$，即可求出m的值，
解答 解：圆锥曲线mx2+y2=1为双曲线，即：${y}^{2}-\frac{{x}^{2}}{-\frac{1}{m}}$=1，
∵圆锥曲线mx2+y2=1的离心率为$\sqrt{2}$，
∴e2=1+$\frac{-1}{m}$=2，∴m=-1．
故选：A．
点评 本题考查双曲线的性质和标准方程，将方程化为标准方程是关键．
练习册系列答案
阅读快车系列答案
相关题目
11．已知a＞0，a≠1，a0.6＜a0.4，设m=0.6loga0.6，n=0.4loga0.6，p=0.6loga0.4，则（ ）
| A． | p＞n＞m | B． | p＞m＞n | C． | n＞m＞p | D． | m＞p＞n |
6．已知l，m是两条不同的直线，α，β是两个不同的平面，下列命题为真命题的序号是（ ）
①若l?α，m?α，l∥β，m∥β，则α∥β；
②若l?α，l∥β，α∩β=m，则l∥m；
③若l∥α，α∥β，则l∥β；
④若l⊥α，l∥m，α∥β，则m⊥β．
①若l?α，m?α，l∥β，m∥β，则α∥β；
②若l?α，l∥β，α∩β=m，则l∥m；
③若l∥α，α∥β，则l∥β；
④若l⊥α，l∥m，α∥β，则m⊥β．
| A． | ①④ | B． | ①③ | C． | ②④ | D． | ②③ |
13．在正三棱柱ABC-A1B1C1中，若AB=BB1，D是CC1中点，则CA1与BD所成角的大小是（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{5π}{12}$ | C． | $\frac{π}{2}$ | D． | $\frac{7π}{12}$ |
如图是某种可固定在墙上的广告金属支架模型，其中AD=6，C是AB的中点，∠BCD=$\frac{π}{3}$，∠BAD=θ（θ∈（$\frac{π}{9}$，$\frac{π}{3}$）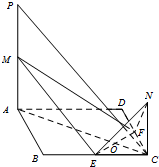
如图，已知E，F分别是正方形ABCD边BC，CD的中点，EF与AC交于点O，PA，NC都垂直于平面ABCD，且PA=AB=2NC，M是PA中点．