题目内容
【题目】已知函数f（x）=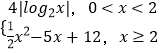 
，若存在实数a、b、c、d，满足f（a）=f（b）=f（c）=f（d），其中d＞c＞b＞a＞0，则abcd的取值范围是（ ）
A.（16，21）
B.（16，24）
C.（17，21）
D.（18，24）
【答案】B
【解析】解：若存在实数a、b、c、d，满足f（a）=f（b）=f（c）=f（d），其中d＞c＞b＞a＞0
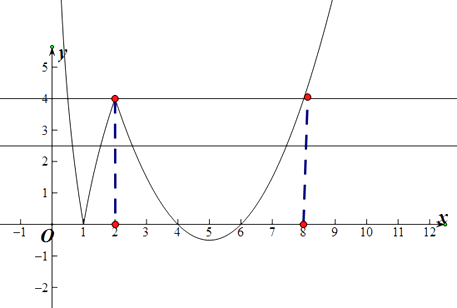
根据图象可判断： 
＜a＜1，1＜b＜2，2＜c＜4，6＜d＜8，
当直线y=t，0＜t＜4，可以有4个交点，把直线向上平移，向下平移，可判断：直线越往上走abcd的积越小，越往下abcd的积越大，
当t=0时1×1×4×6=24，当t=4时， 
=16，abcd的取值范围是（16，24），
故选：B．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】通过市场调查,得到某种产品的资金投入x(单位:万元)与获得的利润y(单位:万元)的数据,如表所示:
资金投入x | 2 | 3 | 4 | 5 | 6 |
利润y | 2 | 3 | 5 | 6 | 9 |
(1)画出数据对应的散点图;
(2)根据上表提供的数据,用最小二乘法求线性回归直线方程
x+
;
(3)现投入资金10万元,求获得利润的估计值为多少万元?
