Question

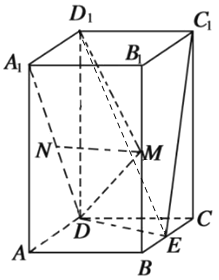
【题目】如图,在直三棱柱ABC—A1B1C1中,ACBC,D,E分别是A1B1,BC的中点．求证：

（1）平面ACD⊥平面BCC1B1；

（2）B1E∥平面ACD．

Answer 1

【答案】（1）见解析（2）见解析

【解析】

(1)根据直三棱柱的性质,证明进而得到平面即可.

(2) 取AC中点F,连结EF,DF,再证明四边形B1DFE为平行四边形即可.

证明：（1）直三棱柱ABC—A1B1C1中,CC1⊥底面ABC,又AC底面ABC

故AC⊥CC1,又因为AC⊥BC,CC1∩BC＝C

CC1平面BCC1B1,BC平面BCC1B1

所以,AC⊥平面BCC1B1,又因为AC平面ACD

所以,平面ACD⊥平面BCC1B1；

（2）取AC中点F,连结EF,DF

因为E,F分别为BC,AC中点

所以,EF∥AB,EF＝AB

三棱柱ABC—A1B1C1中,AB// A1B1,AB＝A1B1

又因为D为A1B1中点,所以B1D∥AB,B1D＝AB

所以,EF∥B1D,EF＝B1D

因此,四边形B1DFE为平行四边形

所以B1E//DF,又因为DF平面ACD,B1E平面ACD

所以,B1E∥平面ACD．