题目内容
【题目】如图,真四棱柱![]() 的底面是菱形,
的底面是菱形,![]() ,
,![]() ,
,![]() ,E,M,N分别是BC,
,E,M,N分别是BC,![]() ,
,![]() 的中点.
的中点.
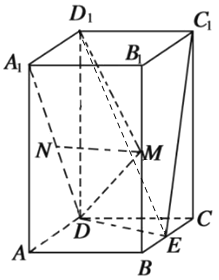
(1)证明:![]() 面
面![]() ;
;
(2)求平面DMN与平面![]() 所成锐角的正切值.
所成锐角的正切值.
【答案】(1)证明见解析.(2)![]()
【解析】
(1)由余弦定理可得![]() ,进而可得
,进而可得![]() ,由正棱柱的几何特征可得
,由正棱柱的几何特征可得![]() ,由线面垂直的判定即可得解;
,由线面垂直的判定即可得解;
(2)连接ME,由题意可得四边形DNME为平行四边形,DE即为平面DMN与平面![]() 的交线,由线面垂直的判定可得
的交线,由线面垂直的判定可得![]() 面
面![]() ,进而可得
,进而可得![]() 即为平面DMN与平面
即为平面DMN与平面![]() 所成的平面角,即可得解.
所成的平面角,即可得解.
(1)证明:∵在菱形ABCD中,![]() ,
,![]() ,且E为BC中点,
,且E为BC中点,
∴![]() ,∴
,∴![]() 即
即![]() ,
,
又棱柱![]() 是直四棱柱,∴
是直四棱柱,∴![]() 平面
平面![]() ,∴
,∴![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
∴![]() 面
面![]() ;
;
(2)连接ME,

∵E,M,N分别是BC,![]() ,
,![]() 的中点,
的中点,
∴![]() 且
且![]() ,
,
∴![]() 且
且![]() ,∴四边形DNME为平行四边形,
,∴四边形DNME为平行四边形,
从而可知:DE即为面DMN与面![]() 的交线,
的交线,
∵![]() ,
,![]() ,
,![]() ,∴
,∴![]() 面
面![]() ,
,
∴![]() 且
且![]() ,
,
则![]() 即为平面DMN与平面
即为平面DMN与平面![]() 所成的平面角,
所成的平面角,
在![]() 中,
中,![]() ,
,
故平面DMN与平面![]() 所成锐角的正切值为
所成锐角的正切值为![]() .
.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
【题目】“网购”已经成为我们日常生活中的一部分,某地区随机调查了100名男性和100名女性在“双十一”活动中用于网购的消费金额,数据整理如下:
男性消费金额频数分布表
消费金额 (单位:元) | 0~500 | 500~1000 | 1000~1500 | 1500~2000 | 2000~3000 |
人数 | 15 | 15 | 20 | 30 | 20 |
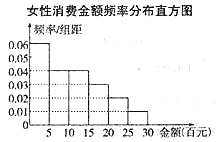
(1)试分别计算男性、女性在此活动中的平均消费金额;
(2)如果分别把男性、女性消费金额与中位数相差不超过200元的消费称作理性消费,试问是否有5成以上的把握认为理性消费与性别有关.
附: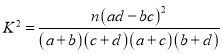
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 |