题目内容

对实数a和b，定义运算“⊗”：a⊗b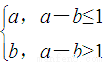＝，设函数f(x)＝(x2－2)⊗(x－x2)，x∈R，若函数y＝f(x)－c的图象与x轴恰有两个公共点，则实数c的取值范围是

A．(－∞，－2]∪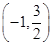　　　　　　　　B．∪ 

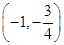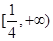
C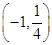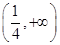．∪　　　　　　　　　D．(－∞，－2]∪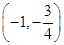

 

 

【答案】

D

【解析】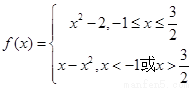,作出其图像，由图像可观察出直线y=c与函数y=f(x)有两个公共点，所以(－∞，－2]∪.

 

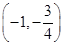练习册系列答案
相关题目
对实数a和b，定义运算“?”：a?b=
a，a≤b
b，a＞b
．设函数f（x）=（x2-1）?（x-x2），x∈R．若函数y=f（x）-c恰有四个不同的零点，则实数c的取值范围是（　　）
对实数a和b，定义运算“?”：a?b=
a，a-b≤1
b，a-b＞1
，设函数f（x）=（x2-2）?（x-x2），x∈R，若函数y=f（x）+c的图象与x轴恰有两个公共点，则实数c的取值范围是
(
3
4
，1)∪[2，+∞)
(
3
4
，1)∪[2，+∞)
．
对实数a和b，定义运算“?”：a?b=
a，a≤b
b，a＞b
设函数f（x）=（x2-1）?（x-x2），x∈R．若函数y=f（x）-c恰有两个不同的零点，则实数c的取值范围是（　　）
对实数a和b，定义运算“⊕”：a⊕b=
a，a≥b
b，a＜b
，设函数f（x）=（x2-1）⊕（x-x2），x∈R，则y=f（x）与x轴的公共点个数为（　　）
（2013•郑州一模）对实数a和b，定义运算“?”；a?b=
a，a-b≤1
b，a-b＞1
设函数f（x）=（x2-2x）?（x-3）（x∈R），若函数y=f（x）-k的图象与x轴恰有两个公共点，则实数k的取值范围是
-1＜k≤0
-1＜k≤0
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网