题目内容
(2013•郑州一模)对实数a和b,定义运算“?”;a?b=
设函数f(x)=(x2-2x)?(x-3)(x∈R),若函数y=f(x)-k的图象与x轴恰有两个公共点,则实数k的取值范围是
|
-1<k≤0
-1<k≤0
.分析:化简函数f(x)的解析式,作出函数y=f(x)的图象,由题意可得,函数y=f(x)与y=k的图象有2个交点,结合图象求得结果.
解答:解:由题意可得f(x)=
=
,
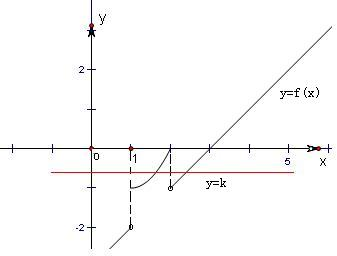 函数y=f(x)的图象如右图所示:
函数y=f(x)的图象如右图所示:
函数y=f(x)-k的图象与x轴恰有两个公共点,即函数y=f(x)与y=k的图象有2个交点.
由图象可得-1<k≤0.
故答案为:-1<k≤0.
|
|
 函数y=f(x)的图象如右图所示:
函数y=f(x)的图象如右图所示:函数y=f(x)-k的图象与x轴恰有两个公共点,即函数y=f(x)与y=k的图象有2个交点.
由图象可得-1<k≤0.
故答案为:-1<k≤0.
点评:本题主要考查根据函数的解析式作出函数的图象,体现了化归与转化、数形结合的数学思想,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2013•郑州一模)执行如图所示的程序框图,若输入x=2,则输出y的值为( )
(2013•郑州一模)执行如图所示的程序框图,若输入x=2,则输出y的值为( )