Question

对实数a和b，定义运算“?”：a?b=

a，a-b≤1 b，a-b＞1

，设函数f（x）=（x²-2）?（x-x²），x∈R，若函数y=f（x）+c的图象与x轴恰有两个公共点，则实数c的取值范围是

(

3

4

，1)∪[2，+∞)

．

Answer 1

分析：根据定义的运算法则化简函数f（x）=（x²-2）?（x-x²）的解析式，并求出f（x）的取值范围，函数y=f（x）+c的图象与x轴恰有两个公共点转化为y=f（x），y=-c图象的交点问题，结合图象求得实数c的取值范围．

解答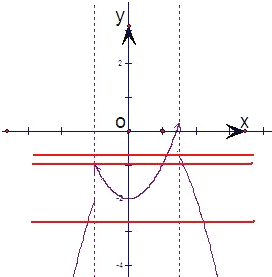：解：∵a?b=

a，a-b≤1 b，a-b＞1.

，
∴函数f（x）=（x²-2）?（x-x²）=

x2-2，-1≤x≤ 3 2 x-x2，x＜-1或x＞ 3 2

，
由图可知，当-c∈(-∞，-2]∪(-1，-

3

4

)，
即c∈(

3

4

，1)∪[2，+∞)
函数f（x） 与y=-c的图象有两个公共点，
∴c的取值范围是 (

3

4

，1)∪[2，+∞)，
故答案为：(

3

4

，1)∪[2，+∞)．

点评：本小题主要考查函数的零点与方程根的关系、不等式的解法等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．