Question

对实数a和b，定义运算“?”：a?b=

a，a≤b b，a＞b

．设函数f（x）=（x²-1）?（x-x²），x∈R．若函数y=f（x）-c恰有四个不同的零点，则实数c的取值范围是（　　）

• A．(-∞，-1)∪(-

  3

  4

  ，0)
• B．[-1，-

  3

  4

  ]
• C．(-1，-

  3

  4

  )
• D．(-∞，-1)∪[-

  3

  4

  ，0)

Answer 1

分析：利用运算“?”的意义即可得到函数f（x）的解析式，画出图象并结合二次函数的单调性即可得出c的取值范围．

解答：解：∵函数f（x）=（x²-1）?（x-x²）=

x2-1，当- 1 2 ≤x≤1时 -x2+x，当x＜- 1 2 或x＞1时

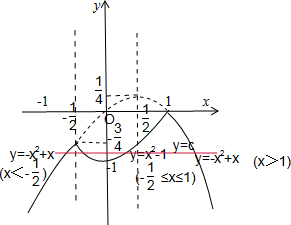
画出图象y=x2-1(-

1

2

≤x≤1)，y=-x2+x=-(x-

1

2

)2+

1

4

 (x＜-

1

4

或x＞1)．
由图象可得：当-1＜c＜-

3

4

时，函数y=c与y=f（x）的图象有四个交点．
即函数y=f（x）-c恰有四个不同的零点时，实数c的取值范围是(-1，-

3

4

)．
故选C．

点评：正确理解新定义和熟练掌握二次函数的图象及其单调性是解题的关键．