Question

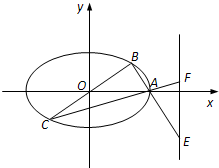在平面直角坐标系xOy中，椭圆

x2

a2

+

y2

b2

=1(a＞b＞0)的离心率为

2

2

，右顶点为A，直线BC过原点O，且点B在x轴上方，直线AB与AC分别交直线l：x=a+1于点E、F．
（1）若点B(

2

，

3

)，求△ABC的面积；
（2）若点B为动点，设直线AB与AC的斜率分别为k₁、k₂．
①试探究：k₁•k₂是否为定值？若为定值，请求出；若不为定值，请说明理由；
②求△AEF的面积的最小值．

Answer 1

分析：（1）根据题意的离心率及点B的坐标，建立方程，求出a的值，即可求△ABC的面积；
（2）①k₁•k₂为定值，证明k1•k2=-

b2

a2

，由（1）得a²=2b²，即可得到结论；
②设直线AB的方程为y=k₁（x-a），直线AC的方程为y=k₂（x-a），令x=a+1得，求出△AEF的面积，结合①的结论，利用基本不等式，可求△AEF的面积的最小值．

解答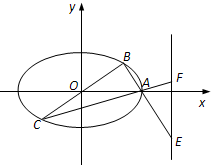：解：（1）由题意得

1- b2 a2 = 2 2 2 a2 + 3 b2 =1

解得a²=2b²=8，
则△ABC的面积S=2S△AOB=2×

1

2

×a×

3

=2

6

；
（2）①k₁•k₂为定值，下证之：
证明：设B（x₀，y₀），则C（-x₀，-y₀），且

x02

a2

+

y02

b2

=1，
而k1•k2=

y0

x0-a

•

y0

x0+a

=

y02

x02-a2

=

b2(1- x02 a2 )

x02-a2

=-

b2

a2

由（1）得a²=2b²，所以k1•k2=-

1

2

；
②设直线AB的方程为y=k₁（x-a），直线AC的方程为y=k₂（x-a），
令x=a+1得，y_E=k₁，y_F=k₂，则△AEF的面积S△AEF=

1

2

×EF×1=

1

2

|k2-k1|，
因为点B在x轴上方，所以k₁＜0，k₂＞0，
由k1•k2=-

1

2

得S△AEF=

1

2

(k2-k1)≥

1

2

×2

-k1k2

=

2

2

（当且仅当k₂=-k₁时等号成立）
所以，△AEF的面积的最小值为

2

2

．

点评：本题主要考查直线的方程、椭圆的方程及其简单性质等基础知识，考查灵活运用数形结合、化归与转化思想进行运算求解、推理论证的能力．