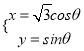Question

【题目】在△ABC中，角A，B，C所对应的边分别为a，b，c，且（2a﹣c）cosB=bcosC． （Ⅰ）求角B的大小；
（Ⅱ）若 ，求△ABC的面积．

Answer 1

【答案】解：（Ⅰ）∵（2a﹣c）cosB=bcosC，由正弦定理，得 ∴（2sinA﹣sinC）cosB=sinBcosC．
∴2sinAcosB=sinCcosB+sinBcosC=sin（B+C）=sinA，
∵A∈（0，π），∴sinA≠0．
∴cosB= ． 又∵0＜B＜π，∴B= ．
（Ⅱ）由正弦定理 ，得 b= =
∵A= ，B= ，∴C= ，∴sinC=sin =sin（ + ）=sin cos +cos sin = ．
∴S= = =
【解析】（Ⅰ）由正弦定理可得 2sinAcosB=sinA，故可得 cosB= ，又0＜B＜π，可得B= ． （Ⅱ）由正弦定理 求得 b= = ，由三角形内角和公式求得 C= ，可得sinC 的值，由此求得S= 的值．