题目内容
若存在实数x满足|x-3|+|x-m|<5,则实数m的取值范围是______.
设f(x)=|x-3|+|x-m|
由于|x-3|+|x-m|≥|x-3-(x-m)|=|m-3|
则f(x)的最小值为|m-3|,
又因为存在实数x满足|x-3|+|x-m|<5,只要5大于f(x)的最小值即可.
即|m-3|<5,解得-2<m<5.
所以m的取值范围是(-2,8).
故答案为:(-2,8).
由于|x-3|+|x-m|≥|x-3-(x-m)|=|m-3|
则f(x)的最小值为|m-3|,
又因为存在实数x满足|x-3|+|x-m|<5,只要5大于f(x)的最小值即可.
即|m-3|<5,解得-2<m<5.
所以m的取值范围是(-2,8).
故答案为:(-2,8).

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目
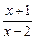 |=
|=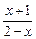 的解集是__________.
的解集是__________.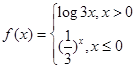 .那么不等式
.那么不等式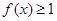 的解集为( ).
的解集为( ).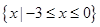
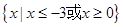
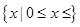

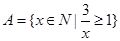 ,
,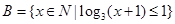 ,
,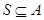 ,
,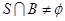 ,则集合
,则集合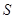 的个数为( )
的个数为( )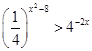 的
的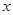 的取值集合是______________.
的取值集合是______________.