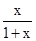题目内容
已知f(x)=|ax+1|(a∈R)|,
(1)a=2时解不等式f(x)≤3;
(2)若|f(x)-2f(
)|≤k恒成立,求k的取值范围.
(1)a=2时解不等式f(x)≤3;
(2)若|f(x)-2f(
| x |
| 2 |
(1)∵a=2时解不等式f(x)≤3化为|2x+1|≤3,
∴-3≤2x+1≤3,
∴-2≤x≤1.
∴解不等式f(x)≤3的解集为[-2,1].
(2)令g(x)=|f(x)-2f(
)|=||ax+1|-2|
x+1||=||ax+1|-|ax+2||,
|f(x)-2f(
)|≤k,只需k≥g(x)max
g(x)=||ax+1|-|ax+2||≤|(ax+1)-(ax+2)|=1,
∴g(x)的最大值为1.
故k的取值范围是[1,+∞).
∴-3≤2x+1≤3,
∴-2≤x≤1.
∴解不等式f(x)≤3的解集为[-2,1].
(2)令g(x)=|f(x)-2f(
| x |
| 2 |
| a |
| 2 |
|f(x)-2f(
| x |
| 2 |
g(x)=||ax+1|-|ax+2||≤|(ax+1)-(ax+2)|=1,
∴g(x)的最大值为1.
故k的取值范围是[1,+∞).

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
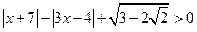
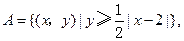
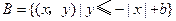 ,
,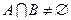 .
. 的取值范围是 ;
的取值范围是 ;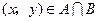 ,且
,且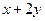 的最大值为9,则
的最大值为9,则