题目内容
已知函数y=f(x)和y=g(x)的定义域均为{x|-2≤x≤2},其图象如图所示:
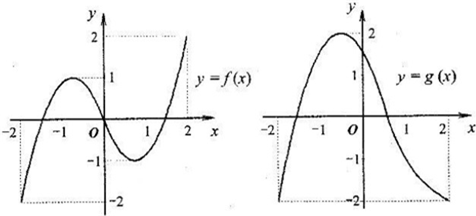
给出下列四个命题:
①函数y=f[g(x)]有且仅有6个零点;
②函数y=g[f(x)]有且仅有3个零点;
③函数y=f[f(x)]有且仅有5个零点;
④函数y=g[f(x)]有且仅有4个零点,其中正确的命题是
- A.①②
- B.①③
- C.②③④
- D.①③④
D
分析:通过f(x)=0可知函数有三个解,g(x)=0有2个解,具体分析 ①②③④推出正确结论.
解答:由图象可得-2≤g(x)≤2,-2≤f(x)≤2,
①由于满足方程f[g(x)]=0 的g(x)有三个不同值,由于每个值g(x)对应了2个x值,
故满足f[g(x)]=0的x值有6个,即方程f[g(x)]=0有且仅有6个根,故①正确.
②由于满足方程g[f(x)]=0的f(x)有2个不同的值,从图中可知,每一个值f(x),
可能对应有1,2,或3个x值,故满足方程g[f(x)]=0的x值可能有2,4,或6个,故②不正确.
③由于满足方程f[f(x)]=0的f(x)有3个不同的值,从图中可知,一个f(x)等于0,
一个f(x)∈(-2,-1),一个f(x)∈(1,2).
而当f(x)=0对应了3个不同的x值;当f(x)∈(-2,-1)时,只对应一个x值;
当f(x)∈(1,2)时,也只对应一个x值.
故满足方程f[f(x)]=0的x值共有5个,故③正确.
④由于满足方程g[g(x)]=0 的g(x)值有2个,而结合图象可得,每个g(x)值对应2个不同的x值,
故满足方程g[g(x)]=0 的x值有4个,即方程g[g(x)]=0有且仅有4个根,故④正确.
故选 D.
点评:本题考查根的存在性及根的个数判断,函数的图象,考查逻辑思维能力及识别图象的能力,是中档题.
分析:通过f(x)=0可知函数有三个解,g(x)=0有2个解,具体分析 ①②③④推出正确结论.
解答:由图象可得-2≤g(x)≤2,-2≤f(x)≤2,
①由于满足方程f[g(x)]=0 的g(x)有三个不同值,由于每个值g(x)对应了2个x值,
故满足f[g(x)]=0的x值有6个,即方程f[g(x)]=0有且仅有6个根,故①正确.
②由于满足方程g[f(x)]=0的f(x)有2个不同的值,从图中可知,每一个值f(x),
可能对应有1,2,或3个x值,故满足方程g[f(x)]=0的x值可能有2,4,或6个,故②不正确.
③由于满足方程f[f(x)]=0的f(x)有3个不同的值,从图中可知,一个f(x)等于0,
一个f(x)∈(-2,-1),一个f(x)∈(1,2).
而当f(x)=0对应了3个不同的x值;当f(x)∈(-2,-1)时,只对应一个x值;
当f(x)∈(1,2)时,也只对应一个x值.
故满足方程f[f(x)]=0的x值共有5个,故③正确.
④由于满足方程g[g(x)]=0 的g(x)值有2个,而结合图象可得,每个g(x)值对应2个不同的x值,
故满足方程g[g(x)]=0 的x值有4个,即方程g[g(x)]=0有且仅有4个根,故④正确.
故选 D.
点评:本题考查根的存在性及根的个数判断,函数的图象,考查逻辑思维能力及识别图象的能力,是中档题.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为 已知函数y=f(x)的图象如图,则满足
已知函数y=f(x)的图象如图,则满足