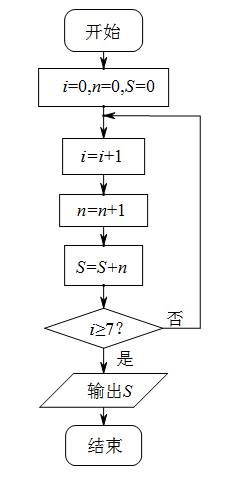
题目内容
【题目】为了丰富学生活动,在体育课上,体育教师设计了一个游戏,让甲、乙、丙三人各抓住橡皮带的一端,甲站在直角![]() 斜边
斜边![]() 的中点
的中点![]() 处,乙站在
处,乙站在![]() 处,丙站在
处,丙站在![]() 处.游戏开始,甲不动,乙、丙分别以
处.游戏开始,甲不动,乙、丙分别以![]() 和
和![]() 的速度同时出发,匀速跑向终点
的速度同时出发,匀速跑向终点![]() 和
和![]() ,运动过程中绷紧的橡皮带围成一个如图所示的
,运动过程中绷紧的橡皮带围成一个如图所示的![]() .(规定:只要有一人跑到终点,游戏就结束,且
.(规定:只要有一人跑到终点,游戏就结束,且![]() ).已知
).已知![]() 长为
长为![]() ,
,![]() 长为
长为![]() ,记经过
,记经过![]() 后
后![]() 的面积为
的面积为![]() .
.
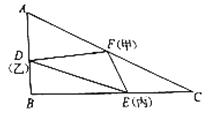
(1)求![]() 关于
关于![]() 的函数表示,并求出
的函数表示,并求出![]() 的取值范围;
的取值范围;
(2)当游戏进行到![]() 时,体育教师宣布停止,求此时
时,体育教师宣布停止,求此时![]() 的最小值.
的最小值.
【答案】(1)![]() ,其中
,其中![]() 时,
时,![]() ,
,![]() 时,
时,![]() .(2)
.(2)![]() 最小值为
最小值为![]()
【解析】
(1)求出路程![]() ,从而可得
,从而可得![]() ,由勾股定理得
,由勾股定理得![]() ,以
,以![]() 为
为![]() 轴建立平面直角坐标系,可得直线
轴建立平面直角坐标系,可得直线![]() 的方程,求出
的方程,求出![]() 到直线
到直线![]() 的距离,即
的距离,即![]() 的高,从而可表示出其面积.计算两人分别走到
的高,从而可表示出其面积.计算两人分别走到![]() 所用时间
所用时间![]() ,比较它们的大小,可得
,比较它们的大小,可得![]() 的取值范围.
的取值范围.
(2)由(1)得![]() ,利用导数求出其最小值.
,利用导数求出其最小值.
解:以![]() 为坐标原点,
为坐标原点,
分别以![]() 、
、![]() 为
为![]() 、
、![]() 轴建立直角坐标系,
轴建立直角坐标系,

![]() ,则
,则![]() ,
,
![]() ,则
,则![]() ,
,
![]() 为
为![]() 中点,则
中点,则![]() ,
,
![]() 秒后
秒后![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
直线![]() 方程为:
方程为:![]() ,
,
![]() ,
,
![]() 到
到![]() 距离
距离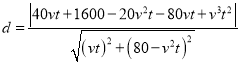
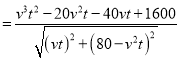 ,
,
∴![]() ,
,
![]() ,即
,即![]() ,则
,则![]() ,
,
![]() ,即
,即![]() ,则
,则![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() ,
,
其中![]() 时,
时,![]() ,
,
![]() 时,
时,![]() .
.
(2)∵![]() ,
,
∴![]() ,
,
![]()
![]() ,
,
令![]() 得
得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 为单调递减,
为单调递减,
当![]() 时,
时,![]() ,
,![]() 为单调递增,
为单调递增,
∴当![]() 时
时![]() 取最小值,
取最小值,
此时![]() ,
,
答:此时![]() 最小值为
最小值为![]() .
.

【题目】2017年9月支付宝宣布在肯德基的KPRO餐厅上线刷脸支付,也即用户可以不用手机,单单通过刷脸就可以完成支付宝支付,这也是刷脸支付在全球范围内的首次商用试点.某市随机抽查了每月用支付宝消费金额不超过3000元的男女顾客各300人,调查了他们的支付宝使用情况,得到如下频率分布直方图:
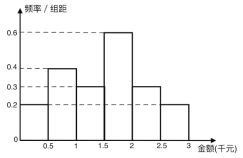
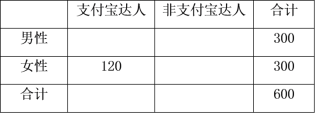
若每月利用支付宝支付金额超过2千元的顾客被称为“支付宝达人”, 利用支付宝支付金额不超过2千元的顾客称为“非支付宝达人”.
(I)若抽取的“支付宝达人”中女性占120人,请根据条件完成上面的![]() 列联表,并判断能否在犯错误的概率不超过0.001的前提下认为“支付宝达人”与性别有关.
列联表,并判断能否在犯错误的概率不超过0.001的前提下认为“支付宝达人”与性别有关.
(II)支付宝公司为了进一步了解这600人的支付宝使用体验情况和建议,从“非支付宝达人” “支付宝达人”中用分层抽样的方法抽取8人.若需从这8人中随机选取2人进行问卷调查,求至少有1人是“支付宝达人”的概率.
附:参考公式与参考数据如下
![]() ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |