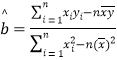题目内容
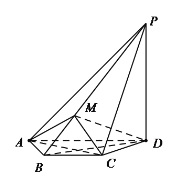
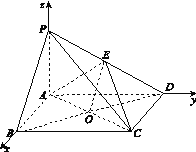
【题目】如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
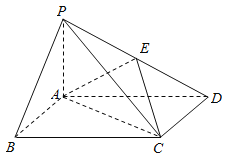
(1) 证明:PB∥平面AEC
(2) 设二面角D-AE-C为60°,AP=1,AD=![]() ,求三棱锥E-ACD的体积
,求三棱锥E-ACD的体积
【答案】![]()
【解析】
试题(Ⅰ)连接BD交AC于O点,连接EO,只要证明EO∥PB,即可证明PB∥平面AEC;(Ⅱ)延长AE至M连结DM,使得AM⊥DM,说明∠CMD=60°,是二面角的平面角,求出CD,即可三棱锥E-ACD的体积
试题解析:(1)证明:连接BD交AC于点O,连接EO.
因为ABCD为矩形,所以O为BD的中点.
又E为PD的中点,所以EO∥PB.
因为EO平面AEC,PB平面AEC,
所以PB∥平面AEC.
(2)因为PA⊥平面ABCD,ABCD为矩形,
所以AB,AD,AP两两垂直.
如图,以A为坐标原点,![]() ,AD,AP的方向为x轴y轴z轴的正方向,|
,AD,AP的方向为x轴y轴z轴的正方向,|![]() |为单位长,建立空间直角坐标系Axyz,则D
|为单位长,建立空间直角坐标系Axyz,则D![]() ,E
,E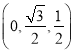 ,
,![]() =
=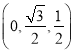 .
.
设B(m,0,0)(m>0),则C(m,![]() ,0),
,0),![]() =(m,
=(m,![]() ,0).
,0).
设n1=(x,y,z)为平面ACE的法向量,
则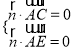 即
即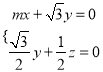
可取n1=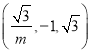 .
.
又n2=(1,0,0)为平面DAE的法向量,
由题设易知|cos〈n1,n2〉|=![]() ,即
,即
![]() =
=![]() ,解得m=
,解得m=![]() .
.
因为E为PD的中点,所以三棱锥EACD的高为![]() .三棱锥EACD的体积V=
.三棱锥EACD的体积V=![]() ×
×![]() ×
×![]() ×
×![]() ×
×![]() =
=![]() .
.

 轻松课堂标准练系列答案
轻松课堂标准练系列答案【题目】某品牌汽车4S店对最近100位采用分期付款的购车者进行统计,统计结果如下表所示:
付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
频数 | 40 | 20 |
| 10 |
|
已知分3期付款的频率为0.2,4s店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元,分2期或3期付款其利润为1.5万元,分4期或5期付款,其利润为2万元,用Y表示经销一辆汽车的利润.
(Ⅰ)求上表中![]() 的值;
的值;
(Ⅱ)若以频率作为概率,求事件![]() :“购买该品牌汽车的3位顾客中,至多有一位采用3期付款”的概率
:“购买该品牌汽车的3位顾客中,至多有一位采用3期付款”的概率![]() ;
;
(Ⅲ)求Y的分布列及数学期望EY.
【题目】“红灯停,绿灯行”,这是我们每个人都应该也必须遵守的交通规则.凑齐一拨人就过马路﹣﹣不看交通信号灯、随意穿行交叉路口的“中国式过马路”不仅不文明而且存在很大的交通安全隐患.一座城市是否存在“中国式过马路”是衡量这座城市文明程度的重要指标.某调查机构为了了解路人对“中国式过马路”的态度,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:
男性 | 女性 | 合计 | |
反感 | 10 | ||
不反感 | 8 | ||
合计 | 30 |
已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是![]() .
.
(1)请将上面的列联表补充完整(在答题卷上直接填写结果,不需要写求解过程),并据此列联表数据判断是否有95%的把握认为反感“中国式过马路”与性别有关?
(2)若从这30人中的女性路人中随机抽取2人参加一项活动,记反感“中国式过马路”的人数为X,求X的分布列及其数学期望.
附:![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |