题目内容
6.设函数f(x)=-$\frac{5}{3}$x3+bx-c,其导数为f′(x),若f′(1)=-2,则二项式(bx+$\frac{1}{x}$)5的展开式中x3的系数为( )| A. | 10250 | B. | 3430 | C. | 825 | D. | 405 |
分析 求函数的导数,根据条件求出b的值,利用二项式定理的知识进行求解即可.
解答 解:函数的导数为f′(x)=-5x2+b,
若f′(1)=-2,
则f′(1)=-5+b=-2,
即b=3,
则二项式(bx+$\frac{1}{x}$)5的展开式的通项公式为Tk+1=${C}_{5}^{k}(bx)^{5-k}•(\frac{1}{x})^{k}$=${C}_{5}^{k}$b5-kx5-k•x-k=${C}_{5}^{k}$b5-kx5-2k,
∵5-2x=3得x=1,
∴展开式中x3的系数为为${C}_{5}^{1}$•b4=5•34=5×81=405,
故选:D.
点评 本题主要考查导数的计算,以及二项式定理的应用,根据导数公式求出b的值是解决本题的关键.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
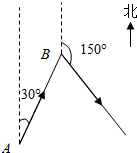 如图所示,已知A、B两点的距离为100海里,B在A的北偏东30°处,甲船自A以50海里/小时的速度向B航行,同时乙船自B以30海里/小时的速度沿方位角150°方向航行.问航行几小时两船之间的距离最短?
如图所示,已知A、B两点的距离为100海里,B在A的北偏东30°处,甲船自A以50海里/小时的速度向B航行,同时乙船自B以30海里/小时的速度沿方位角150°方向航行.问航行几小时两船之间的距离最短?