题目内容
【题目】已知函数![]() ,直线
,直线![]() 是曲线
是曲线![]() 的一条切线.
的一条切线.
(1)求实数a的值;
(2)若对任意的x![]() (0,
(0,![]() ),都有
),都有![]() ,求整数k的最大值.
,求整数k的最大值.
【答案】(1)1(2)3
【解析】
(1)设出切点的坐标,利用斜率和切点在直线上列方程组,解方程组求得切点的坐标以及![]() 的值.(2)构造函数
的值.(2)构造函数![]() ,利用导数证得当
,利用导数证得当![]() 时函数的最小值大于零,当
时函数的最小值大于零,当![]() 函数值的最小值小于零,由此求得
函数值的最小值小于零,由此求得![]() 点的最大整数值为
点的最大整数值为![]() .
.
解:(1)设切点P(m,mlnm+am+1),
由f ′(x)=lnx+1+a
知 f(m)=lnm+1+a.
则在点P处的切线l方程为:y=(lnm+1+a)x-m+1.
若与题目中的切线重合,则必有![]() ,
,
解得a=m=1,
所以a的值为1.
(2) 令F(x)=f(x)-k(x-1),
则根据题意,等价于F(x)>0对任意的正数x恒成立.
F ′(x)=lnx+2-k,
令F ′(x)=0,则x=ek-2 .
当0<x<ek-2 ,则F ′(x)<0,F(x)在(0,ek-2)上单减;
当x>ek-2 ,则F ′(x)>0,F(x)在(ek-2,+∞)上单增.
所以有F(x)![]() =F(ek-2) >0,即ek-2-k-1<0.
=F(ek-2) >0,即ek-2-k-1<0.
当k=3,容易验证,ek-2-k-1<0;
下证:当k≥4,ek-2-k-1>0成立.
令h(x)=ex-2-x-1,x≥4,
则h ′(x)=ex-2-1≥0,对任意的x≥4恒成立。
于是h(x)在[4,+∞)上单增,
故h(x)![]() =h(4)=e2-5>0;
=h(4)=e2-5>0;
所以对于任意的x≥4,ex-2-x-1>0.
综上,k的最大值为3.

【题目】![]() 是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物).为了探究车流量与
是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物).为了探究车流量与![]() 的浓度是否有关,现采集到某城市周一至周五某一时间段车流量与
的浓度是否有关,现采集到某城市周一至周五某一时间段车流量与![]() 的浓度的数据如下表:
的浓度的数据如下表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量 | 100 | 102 | 108 | 114 | 116 |
| 78 | 80 | 84 | 88 | 90 |
(1)根据上表数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若周六同一时间段车流量是200万辆,试根据(1)求出的线性回归方程,预测此时![]() 的浓度为多少.
的浓度为多少.
参考公式: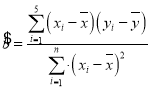 ,
,![]() .
.
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人.第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:
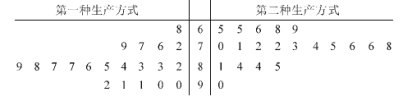
(1)求40名工人完成生产任务所需时间的中位数m,并将完成生产任务所需时间超过m和不超过m的工人数填入下面的列联表:
超过m | 不超过m | 总计 | |
第一种生产方式 | |||
第二种生产方式 | |||
总计 |
(2)根据(1)中的列联表,能否有![]() 的把握认为两种生产方式的效率有差异?
的把握认为两种生产方式的效率有差异?
附: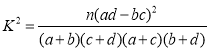
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |