Question

（08年安徽信息交流）（本小题满分14分）已知两定点A（，0），B（3，0），动圆M与直线AB相切于点N．且=4，现分别过点A、B作动圆M的切线（异于直线AB），两切线相交于点P．

（1）求动点P的轨迹方程；

（2）若直线截动点P的轨迹所得的弦长为5，求m的值；

（3）设过轨迹上的点P的直线与两直线，分别交于点，，且点分有向线段所成的比为（＞0），当∈时，求的最小值与最大值。

Answer 1

解析:（1）由题设及平面几何知识得：＜,

∵动点P的轨迹是以A、B为交点的双曲线右支，

由

故所求P点的轨迹方程为：  （4分）

（2）易知 直线恒过双曲线焦点B（3，0）

设该直线与双曲线右支相交于

由双曲线第二定义知，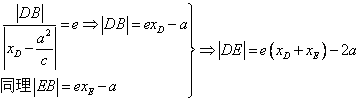

又∴，则，

由得，从而易知，仅当时，满足

故所求  （8分）

（3）设，且p分有向线段所成的比为，

则，，

又点在双曲线上，∴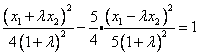

化简得：

又 

∴                               （11分）

令

∵在上单减，在上单增，

又，∴在上单减，在上单增，∴

又 ，∴

故所求的最小值为9，最大值为。   （14分）