题目内容
【题目】如果无穷数列{an}满足条件：①
；② 存在实数M，使得an≤M，其中n∈N*，那么我们称数列{an}为Ω数列.
（1）设数列{bn}的通项为bn＝20n－2n，且是Ω数列，求M的取值范围；
（2）设{cn}是各项为正数的等比数列，Sn是其前n项和，c3＝
，S3＝
，证明：数列{Sn}是Ω数列；
（3）设数列{dn}是各项均为正整数的Ω数列，求证：dn≤dn＋1.
【答案】（1）
；（2）证明见解析；（3）证明见解析
【解析】
（1）求出数列
的最大项即可得；
（2）由等比数列的基本量法求出
，根据数列新定义证明即可；
（3）用反证法，假设存在正整数
，使得
，由数列{dn}是各项均为正整数得
，即
.然后利用新定义归纳
，这样由
可得数列从某一项开始为负．与已知矛盾．从而证得结论．
解：（1）因为bn＝20n－2n，所以
，
所以当
时，
；当
时，
，
所以数列{bn}的最大项是
，
所以
，所以M的取值范围是.
（2）设{cn}的公比为
，则
，c3＝
，
整理得
，解得
或
，因为
，所以.
因为{cn}是等比数列，所以
所以
.
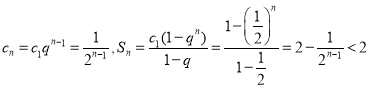因为
，所以数列{Sn}是Ω数列.
（3）假设存在正整数，使得，由数列{dn}是各项均为正整数得，即.
因为数列{dn}是Ω数列，所以
，
所以
，
同理，
，
依此类推，得.
因为数列{dn}是Ω数列，所以存在
，，所以当
时，
，与数列{dn}各项均为正整数矛盾，所以假设不成立，即对任意的正整数
，dn≤dn＋1
练习册系列答案
阅读快车系列答案
相关题目
