题目内容
16．
如图，在四边形ABCB′，△ABC≌△AB′C，AB⊥AB′，cos∠BCB′=$\frac{3}{4}$，BC=2$\sqrt{2}$．（1）求sin∠BCA；
（2）求BB′及AC′的长．
分析 （1）利用△ABC≌△AB′C，可得∠BCA=∠B′CA，利用cos∠BCB′=$\frac{3}{4}$，即可求sin∠BCA；
（2）利用余弦定理求出BB′，利用正弦定理求出BB′，即可求出AC′的长．
解答 解：（1）∵△ABC≌△AB′C，
∴∠BCA=∠B′CA，
∴cos∠BCB′=2cos2∠BCA-1，
∵cos∠BCB′=$\frac{3}{4}$，
∴cos2∠BCA=$\frac{7}{8}$，
∴sin2∠BCA=$\frac{1}{8}$，
∴sin∠BCA=$\frac{\sqrt{2}}{4}$；
（2）∵BC=2$\sqrt{2}$，
∴BB′2=8+8-2×$2\sqrt{2}×2\sqrt{2}×\frac{3}{4}$=4，
∴BB′=2
∵$\frac{AB}{sin∠BCA}=\frac{BC}{sin45°}$，∴AB=$\sqrt{2}$，
设BB′与AC交于O，则AO=1，CO=$\sqrt{8-1}$=$\sqrt{7}$，∴AC=$\sqrt{7}$+1．
点评 本题考查二倍角公式，考查余弦定理，考查正弦定理，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
6．圆C1：（x-1）2+（y-1）2=1关于直线x+y=0对称的圆C2的方程为（ ）
| A． | （x+1）2+（y-1）2=1 | B． | （x-1）2+（y+1）2=1 | ||
| C． | （x+1）2+（y+1）2=1 | D． | （x+1）2+（y-1）2=1或（x-1）2+（y+1）2=1 |
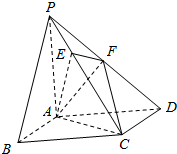如图，四棱锥P-ABCD的底面ABCD是正方形，PA⊥平面ABCD，AP=AD=1，点E在PC上，且PE=$\frac{1}{2}$EC，点F是PD的中点．