题目内容
在三棱锥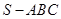 中,
中,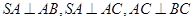 且
且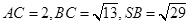 .
.
(Ⅰ)求证: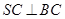 ;
;
(Ⅱ)求三棱锥的体积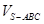 .
.
(Ⅰ)证明过程详见试题解析;(Ⅱ)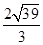 .
.
解析试题分析:(Ⅰ)由线线垂直得到线面垂直,再根据直线所在的平面得到线线垂直;(Ⅱ)根据三棱锥的体积公式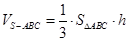 求之.
求之.
试题解析:(Ⅰ)证明:因为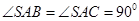 ,所以
,所以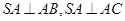 .
.
又因为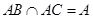 ,所以
,所以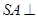 平面
平面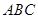 ,所以
,所以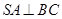 .
.
又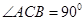 ,所以
,所以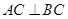 .所以
.所以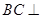 平面
平面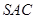 .故
.故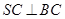 .
.
(Ⅱ)在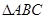 中,
中,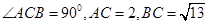 ,所以
,所以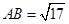 .
.
又在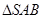 中,
中,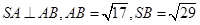 ,所以
,所以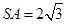 .
.
又因为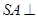 平面
平面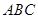 ,所以
,所以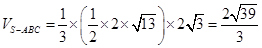 .
.
考点:(Ⅰ)线面垂直的性质定理;(Ⅱ)三棱锥的体积公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
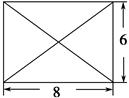
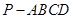 中,底面
中,底面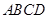 为直角梯形,且
为直角梯形,且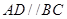 ,
,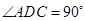 ,平面
,平面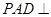 底面
底面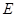 为
为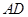 的中点,
的中点,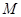 是棱
是棱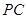 的中点,
的中点, .
.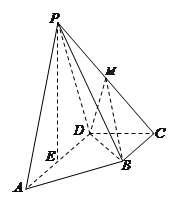

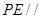 平面
平面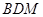 ;
;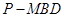 的体积.
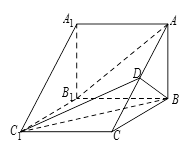
的体积. 中,AC⊥BC,AB⊥
中,AC⊥BC,AB⊥ ,
,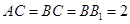 ,D为AB的中点,且CD⊥
,D为AB的中点,且CD⊥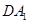 。
。
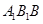 ⊥平面ABC;
⊥平面ABC; 的体积。
的体积。 和AB1的中点,点F在BC上且满足BF∶FC=1∶3.
和AB1的中点,点F在BC上且满足BF∶FC=1∶3.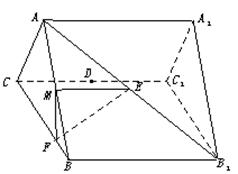
 的体积.
的体积. 平面ABCD,四边形ABCD为矩形,PA=AB=
平面ABCD,四边形ABCD为矩形,PA=AB= ,AD=1,点F是PB的中点,点E在边BC上移动.
,AD=1,点F是PB的中点,点E在边BC上移动.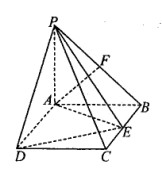
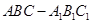 中,侧棱
中,侧棱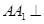 底面
底面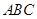 ,
,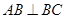 ,
,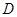 为
为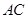 的中点,
的中点,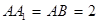 .
.
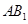 //平面
//平面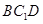 ;
;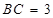 ,求四棱锥
,求四棱锥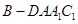 的体积.
的体积. 中,
中,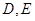 分别为
分别为 、
、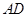 的中点,
的中点, 为
为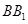 上的点,且
上的点,且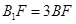
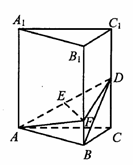
 ∥平面
∥平面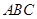 ;
;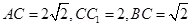 ,
, ,求三棱锥
,求三棱锥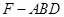 的体积.
的体积.