题目内容
3.利用三角函数线求满足tanα≥$\frac{\sqrt{3}}{3}$的角α的范围.分析 先作出单位圆,由已知条件求出角在[0,2π)的取值范围,再利用终边相同的角的概念,求出满足tanα≥$\frac{\sqrt{3}}{3}$的角α的范围.
解答 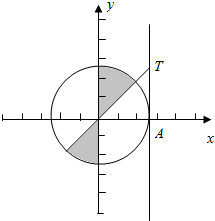 解:∵tanα≥$\frac{\sqrt{3}}{3}$,
解:∵tanα≥$\frac{\sqrt{3}}{3}$,
∴作出单位圆如下:
结合单位圆得到$\frac{π}{6}≤α<\frac{π}{2}$或$\frac{7π}{6}≤α<\frac{3π}{2}$,
∴满足tanα≥$\frac{\sqrt{3}}{3}$的角α的范围是[$kπ+\frac{π}{6}$,$kπ+\frac{π}{2}$),k∈Z.
点评 本题考查角的取值范围的求法,是基础题,解题时要认真审题,注意单位圆和正切线的性质的合理运用.

练习册系列答案
相关题目
13.已知p:?x∈R,x2-x+1>0,q:?x∈(0,+∞),sinx>1,则下列命题为真命题的是( )
| A. | p∧q | B. | ¬p∨q | C. | p∨¬q | D. | ¬p∧¬q |
14.若sinα=-$\frac{\sqrt{10}}{10}$,且α为第四象限角,则tanα的值等于( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | -3 |
15.sin2(π+α)-cos(π+α)cosα+1的值是( )
| A. | 2 | B. | 1 | C. | 2sin2α | D. | 0 |
14.已知m∈R,函数f(x)=$\left\{\begin{array}{l}{|x+1|,}&{x<1}\\{lg(x-1),}&{x>1}\end{array}\right.$,g(x)=x2-2x+2m-2,若函数y=f(g(x))-m有6个零点,则实数m的取值范围是( )
| A. | (1,2) | B. | ($\frac{3}{4}$,1) | C. | ($\frac{2}{3}$,$\frac{3}{4}$) | D. | (0,$\frac{2}{3}$) |