题目内容
【题目】已知函数
（
，且
）在
上单调递增，且关于
的方程
恰有两个不相等的实数解，则
的取值范围是（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】
由题意首先求得a的取值范围，然后结合函数的解析式将原问题转化为两函数图像存在两个交点的问题，数形结合即可确定a的取值范围.
由函数的解析式可知函数在区间
上单调递增，
当
时，函数
单调递减，由复合函数的单调性法则可知：
，
且函数在
处满足：
，解得：
，故
，
方程
恰有两个不相等的实数解，则函数
与函数
的图像有且仅有两个不同的交点，
绘制函数的图像如图中虚线所示，
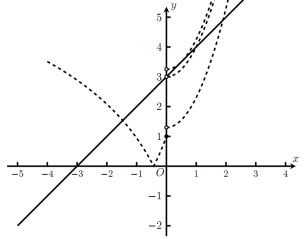
令
可得：
，
由可知
，
，
则直线与函数的图像在区间
上存在唯一的交点，
原问题转化为函数与二次函数
在区间上存在唯一的交点，
很明显当
，即
时满足题意，
当直线与二次函数相切时，设切点坐标为
，亦即
，
由函数的解析式可得：
，故：
，则
，
切点坐标为
，从而：
，即
.
据此可得：
的取值范围是
.
故选：D.
练习册系列答案
相关题目
